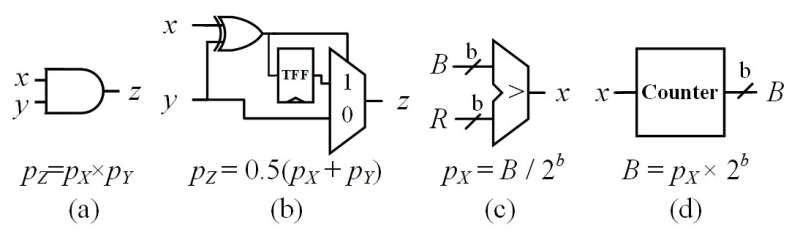
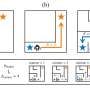
An example of stochastic computing circuits. SC circuits: (a) multiplier, (b), scaled adder, (c) digital-to-stochastic converter, and (d) stochastic-to-digital converter. Credit: Lee et al.
Researchers at the University of Washington have recently developed a new technique to automate the synthesis of stochastic computing (SC) circuits. Their method, presented in a paper pre-published on arXiv, is based on stochastic synthesis, which is traditionally a program synthesis technique.
Stochastic computing (SC) is an emerging and unconventional computation method that encodes data as probabilistic bit streams, making designing new circuits unintuitive. SC could achieve higher computational density and lower power consumption than traditional binary-encoded (BE) computation methods.
"One of the key challenges in stochastic computing research is identifying new ways to design new stochastic circuits," Vincent Lee, one of the researchers who carried out the study, told TechXplore. "The amount of engineering effort and insight that goes into designing a new class of stochastic circuits is fairly high, so finding new, automated ways to reduce the design burden has been an ongoing research objective of mine."
Existing methods for synthesizing SC circuits are typically limited to specific types or classes of functions, such as polynomial evaluation or constant scaling. Lee and his colleagues set out to identify a more effective method to synthesize SC circuits, which could have more widespread applications.
"I came across stochastic synthesis in our program synthesis reading group, while reading a paper by Eric Schkufza et al.," Lee said. "I was new to the area of program synthesis and I thought it was very cool how it could solve optimization tasks where the solutions were fairly unintuitive or difficult for designers or programmers to get right. Despite some scalability limitations, the problem I had, designing new stochastic circuits, tended to have small solutions, so I thought stochastic synthesis could be a good match."
The method devised by Lee and his colleagues is an adaptation of the core stochastic synthesis algorithm that supports circuits instead of programs. The general idea behind it is to treat all circuits as a high dimensional space in which each circuit is given a specific cost.
This cost is defined by a cost function, capturing how effective a circuit is in relation to other circuits in the space. In their study, the researchers set the cost function to measure error, in respect to a specification that defines what they wanted the circuit to do.
"The technique then traverses the space of circuits toward circuits with better cost, similar to how gradient descent moves toward parameter sets that better optimize the objective function," Lee explained. "This provides a more intelligent search over the space of circuits, synthesizing promising circuits faster than if you tried brute-force enumeration or randomly enumerated solutions."
The researchers evaluated their technique and compared it to other existing methods for synthesizing SC circuits. They found stochastic synthesis to be more general than current methods, effectively synthesizing both manually designed and new SC circuits.
"I think the most meaningful results of our study are that the technique is able to synthesize new circuits which would have been unintuitive to design by hand," Lee said. "Being able to automatically generate a stochastic circuit solely based on a specification describing its functionality is a pretty exciting development in stochastic computing."
The findings gathered by Lee and his colleagues suggest that stochastic synthesis could help to automate the task of synthesizing SC circuits. This would ultimately relieve SC designers of a significant design burden, allowing them to focus on other tasks.
"Even if the technique does not return a good quality solution, it may return a circuit that implements a reasonable approximation, or insight into types of circuits that may be worth further evaluations," Lee said. "In this work, we actually found a number of interesting circuits that used a microarchitecture we had never even considered before, which was also pretty exciting."
One of the key challenges that the researchers encountered in their study is scalability. In fact, the efficiency of their technique's search (i.e. the quality of the solution given a fixed search time budget and the time it takes for it to identify correct solutions) is sensitive to the cost function, as this is what defines the gradient and how the search traverses over the circuit space.
"Fortunately, most desirable stochastic circuits are relatively small, so scalability is not crucial to the practicality of the technique," Lee said. "However, this observed limitation leaves a lot of opportunity to improve the efficiency of the technique with heuristics, allowing it to scale to larger circuits. I think this would be an interesting area to explore in our future work."
More information: Stochastic synthesis for stochastic computing. arXiv: 1810.04756v1 [cs.ET]. arxiv.org/pdf/1810.04756.pdf
Stochastic superoptimization. DOI: 10.1145/2499368.2451150. dl.acm.org/citation.cfm?id=2451150
© 2018 Tech Xplore