Credit: CC0 Public Domain
In the communication systems, communication signals usually go through multiple paths from the transmitter to the receiver, during which inter-symbol interference (ISI) is introduced into the received signals. Channel equalization is the main technique to eliminate the ISI.
In theory, the maximum a posteriori (MAP) equalizer is optimal, but its complexity increases exponentially with the channel length. Researchers usually design the channel equalizer based on the minimum mean-squared error (MMSE) criterion. However, these equalizers have large performance loss.
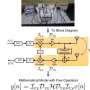
In order to enable the low-complexity optimal equalization, researchers from the Institute of Acoustics (IOA) of the Chinese Academy of Sciences and Southeast University proposed a Hadamard-Haar random precoding (HHRP) scheme, and obtained near-optimal performance with a linear complexity based on the vector approximate message passing (VAMP) algorithm on the receiver side.
They proposed an HHRP scheme that concatenates the Hadamard-Haar transform (HHT), random symbol-interleaver, and the fast Fourier transform.
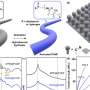
The HHRP enabled a right-rotationally invariant (RRI) channel matrix, which was a necessary condition for the VAMP to achieve the Bayes optimal estimation. Meanwhile, it brought the time and frequency diversities, facilitating symbol detection. In addition, the self-iterative HHRP-VAMP equalizer incurred linear complexity since the HHT could be implemented by only addition operations.
Simulation results showed that under the severe frequency-selectivity Proakis C channel, both the performance and the convergence of the HHRP-VAMP equalizer were comparable with the optimal MAP equalizer and were superior to other existing VAMP equalizers.
More information: Dong Li et al. Near-Optimal Self-Iterative VAMP Equalization enabled by Hadamard-Haar Random Precoding, IEEE Communications Letters (2020). DOI: 10.1109/LCOMM.2020.2981073
Provided by Chinese Academy of Sciences