Theoretical study shows how to make wireless localization much more accurate
With billions of GPS devices in use today, people are beginning to take it for granted that services on their handheld devices will be location-aware.
But GPS doesn't work well indoors, and it's not precise enough for several potentially useful applications, such as locating medical equipment in hospitals or pallets of goods in warehouses, or helping emergency responders navigate unfamiliar buildings.
Professor of aeronautics and astronautics Moe Win has spent the last decade investigating the theory and practice of using wireless signals to gauge location. In 2010, his group published a series of papers deriving fundamental limits on the accuracy of systems that infer wireless transmitters' locations based on features of their signals, such as power, angle of arrival, and time of flight.
In the February issue of the journal IEEE Transactions on Information Theory, Win and two colleagues—Wenhan Dai, an MIT graduate student in aeronautics and astronautics, and Yuan Shen, an associate professor of electronic engineering at Tsinghua University, who did his graduate work at MIT—expand on those results.
First, they show how changing a wireless localization system's parameters—such as the power, bandwidth, and duration of its transmissions—alters the fundamental limits on its accuracy. This, in turn, allows them to determine the system configuration that yields the most accurate location inferences. They also provide practical localization algorithms that can approach those limits in real-world scenarios.
"We are developing a theory to determine the fundamental limits of location inference within different sets of constraints," Win says. "In other words, what's the best we can do with given resources? Based on the theory, we develop algorithms that approach these limits, and then we go into experimentation. The fact that we have the goal of going to experimentation means that the algorithms have to be as efficient as possible."
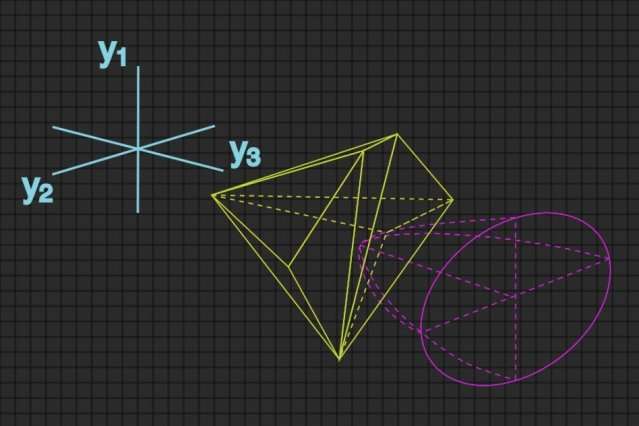
Geometrical thinking
The researchers' theoretical approach assumes that the localization network consists of nodes with known positions, referred to as "anchors," and nodes with unknown positions, referred to as "agents." Wi-Fi access points distributed through an office building, for instance, could serve as anchors. Smartphones trying to determine their positions relative to the anchors would count as agents.
Within the theoretical framework, the goal is something the researchers call "node prioritization"—that is, determining which of the available anchors should transmit, at what power and with what range of frequencies and signal durations, in order to achieve a balance between localization accuracy and consumption of system resources. A solution that produced very accurate measurements by allowing an anchor to blast so loud and long that no other communication over the network was possible, for instance, would not be considered optimal.
The researchers' theoretical analysis shows that the ability to adjust system parameters can consistently reduce localization error by 30 to 50 percent.
The key to the new paper is a geometric interpretation of the problem of choosing and configuring anchors. The metric that the researchers use to assess the accuracy of location inferences depends on three different characteristics of the location information extracted from wireless signals. As such, it defines a three-dimensional mathematical space, which turns out to be bullet-shaped.
The possible settings of all the anchors in the network also define a mathematical space, which is typically much larger. If the network has 20 anchors, then the corresponding settings define a 20-dimensional space. Win, Dai, and Shen, however, found a way to transform the high-dimensional space into a three-dimensional one: a polyhedron that represents all possible anchor configurations that meet certain resource constraints. Transposing both sets of data into the same three-dimensional space makes calculating the solution to the node prioritization problem much simpler and faster.
The problem becomes finding the bullet—a representation of the localization error metric—that intersects the polyhedron at exactly one point. This point represents the network configuration that will provide the most accurate location inference. If the bullet and the polyhedron don't intersect at all, then the error measurement is unachievable. If they overlap, then the error measurement is not as low as it could be. Once the point of intersection has been identified, it can be mapped back on to the higher-dimensional space, where it represents particular anchor settings.
Close enough
This method is particularly effective if the network's resource constraints—in terms of transmission power, bandwidth, and duration—are treated as a single cumulative value. In this case, finding the point of intersection between the polyhedron and the bullet is computationally practical.
In real-world circumstances, however, the limitations of the nodes may need to be considered individually. In that case, the shape of the polyhedron becomes more complex, and finding the point of intersection becomes more time consuming.
To address this scenario, Win, Dai, and Shen also present an approximate algorithm for network configuration with individually constrained devices. In the paper, they were able to show that, while the approximate algorithm is much faster, its results are virtually indistinguishable from those of the full-blown optimization algorithm.
More information: Yuan Shen et al. Fundamental Limits of Wideband Localization— Part II: Cooperative Networks, IEEE Transactions on Information Theory (2010). DOI: 10.1109/TIT.2010.2059720
This story is republished courtesy of MIT News (web.mit.edu/newsoffice/), a popular site that covers news about MIT research, innovation and teaching.


















