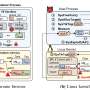
Mathematical verification tests if software runs as advertised

When it comes to security, what you don't know can hurt you.
Most people never think about the encryption that underlies secure online activities including banking, shopping and communications. But all rely on computer programs to generate a random number that serves as a key to unlock encrypted communication. The problem is that small programming errors can make these systems vulnerable, and those vulnerabilities can often be very difficult to detect.
"Whenever you connect up to Amazon to give them your credit card number, whenever you log in somewhere through a secure connection, you're depending on randomly generated cryptographic keys," said Andrew Appel, the Eugene Higgins Professor of Computer Science at Princeton. "And if the adversary, the spy who is trying to read your messages or impersonate you, could guess what random number your computer was using, then it could know what key you're going to be using and it could impersonate your traffic and read your messages."
Appel's research has long focused on the intersection of computing and public policy. He has written extensively about voting machine technology and has testified before Congress on methods for securing the U.S. election system. In recent work, his research has focused on formal verification, a set of tools "for specifying what programs should do, for building programs that conform to those specifications, and for verifying that programs do behave exactly as specified," according to the website of DeepSpec, a multi-institution project that Appel leads.
In one example of mathematically checking the correctness of a critical function, Appel's group developed a method to verify the strength of random number generators that form the basis of most encryption systems. In a paper that grew from the senior thesis work of Katherine Ye '16, the team (which also included researchers at Johns Hopkins University and Oracle) examined a commonly used random number generator and produced a comprehensive and machine-checked proof that the system is indeed secure. Conventional methods such as exhaustive testing cannot tell whether a random number generator is secure.
Commenting on the work, Eugene Spafford, a leader in information security and assurance at Purdue University, said the research is a significant advance. "Like a lot of other research, it may not directly apply to your life and mine at the moment, but it's building up a set of results that could [lead to] very important results in the future."
More information: Katherine Q. Ye et al. Verified Correctness and Security of mbedTLS HMAC-DRBG, Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security - CCS '17 (2017). DOI: 10.1145/3133956.3133974