September 6, 2019 feature
Simulating quantum many-body systems on Amazon Web Services
Quantum many-body systems (QMBs), which are physical systems made up of multiple interacting particles, are among the most challenging structures to reproduce in numerical simulations. In the past, researchers have attempted to simulate these systems using a variety of techniques, including Monte Carlo simulations and even exact diagonalizations.
Methods involving tensor networks (TNs), mathematical concepts that can be applied in a variety of scientific fields, have also shown some potential for the simulation of QMBs. However, so far, these techniques have only been successfully applied to small systems or those with a simple geometry.
In a recent study, researchers at the University of Central Florida were able to simulate QMBs on Amazon Web Services using a TN-based method. Their paper, pre-published on arXiv, highlights some of the potential advantages and implications of using cloud services for research purposes.
"The main motivation behind this work was to demonstrate that the advances in cloud computation services provide a reasonable alternative to other HPC platforms in the context of QMB simulations," Justin Reyes, one of the researchers who carried out the study, told TechXplore. "However, this is true only if we design our QMB algorithms to be multi-threaded according to the system's geometry."
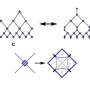
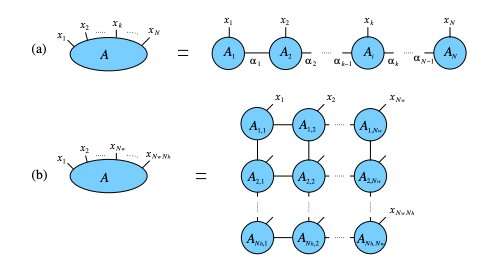
In their research, Reyes and his colleagues decided to use a TN-based approach, which is currently the leading technique used for QMB simulation, especially in studies aimed at determining quantum phase transitions (e.g., when the zero-temperature state of a system goes from being magnetic to nonmagnetic due to quantum fluctuations). To extract information from TNs, researchers need to carry out a procedure known as tensor contraction.
Previous studies have struggled to apply TN-based methods to QMB simulation primarily due to the fact that this 'contraction' procedure is an NP-hard problem. This essentially means that it is a type of computational problem that is extremely difficult to solve.
"Even searching for the optimal contraction order was found to be an NP-hard problem," Reyes said. "We thus approached the problem by selecting a specific geometry on a paradigmatic system, the Ising model in the presence of a transverse magnetic field, with everything following from that starting point."
The Ising model is a mathematical construct used to describe ferromagnetism in the field of statistical mechanics. In their study, the researchers applied their TN-based technique to this specific model by taking a graph of tensors and partitioning it across multiple threads according to the graph geometry on Amazon Web Services (AWS) instances with the largest memories.
"This was done to mitigate communication costs, which proved to be advantageous," Reyes explained. "The only drawback on this approach currently is that it is limited to the largest cache available, as nothing is stored on disc to limit computational costs."
When Reyes and his colleagues reviewed previous academic literature in the field, they found no instances in which research teams had chosen to partition tensors according to the lattice structures. Most researchers had instead decided to subdivide each tensor that was assigned to an individual spin or lattice site. Using the method developed by Reyes and his colleagues, on the other hand, groups of sites or tensors were partitioned into various threads according to the lattice geometry.
"Their initial tensor elements were set to mimic a uniform quantum superposition of all possible system states and an imaginary time evolution algorithm was used to update the tensors iteratively until convergence at the ground state energy was reached," Reyes said. "Our primary concern was not the simulation of this particular model, as it is paradigmatic and well known, but rather that the method used to achieve the results is unique and demonstrably efficient."
The study carried out by Reyes and his colleagues demonstrates the feasibility of using cloud services and TN-based approaches to simulate QMBs. Contrarily to previously proposed methods, their approach distributes the tensors over multiple threads. This partitioning of tensors, however, should also take into account the high communication latency associated with cloud services.
"In the past, QMB problems exhibit fine-grain parallelism and have been solved using supercomputers because they are CPU-, memory- and communication-intensive, and computer clouds target primarily enterprise applications," Dr. Dan Marinescu, another researcher involved in the study, told TechXplore. "Most importantly, cloud interconnection networks have larger communication latency. All these considerations required a carefully designed algorithm that minimizes communication."
The researchers hope that their findings will encourage other teams worldwide to move more research onto the cloud, as this could be far more cost effective than purchasing a personal computer cluster or managing an account with an HPC cluster provider. In their future studies, Reyes and his colleagues plan to explore different geometries for tensor networks.
"We will also seek out a way to merge the partitioning of individual sensors (as in other approaches) with the partitioning according to lattice geometry introduced in our study," Reyes added. The former will allow for larger systems, while the latter takes advantage of the cloud infrastructure for parallel computations."
More information: Simulation of quantum many-body systems on Amazon Cloud. arXiv:1908.08553 [cs.DC]. arxiv.org/abs/1908.08553
© 2019 Science X Network