Statistical solution to processing very large datasets efficiently with memory limit
Any high-performance computing should be able to handle a vast amount of data in a short amount of time—an important aspect on which entire fields (data science, Big Data) are based. Usually, the first step to managing a large amount of data is either to classify it based on well-defined attributes or—as is typical in machine learning—"cluster" them into groups such that data points in the same group are more similar to one another than to those in another group. However, for an extremely large dataset, which can have trillions of sample points, it is tedious to even group data points into a single cluster without huge memory requirements.
"The problem can be formulated as follows: Suppose we have a clustering tool that can process up to lmax samples. The tool classifies l (input) samples into M(l) groups (as output) based on some attributes. Let the actual number of samples be L and G = M(L) be the total number of attributes we want to find. The problem is that if L is much larger than lmax, we cannot determine G owing to limitations in memory capacity," explains Professor Ryo Maezono from the Japan Advanced Institute of Science and Technology (JAIST), who specializes in computational condensed matter theory.
Interestingly enough, very large sample sizes are common in materials science, where calculations involving atomic substitutions in a crystal structure often involve possibilities ranging in trillions. However, a mathematical theorem called Polya's theorem, which uses the symmetry of the crystal, often simplifies the calculations to a great extent. Unfortunately, Polya's theorem only works for problems with symmetry and is, therefore, of limited scope.
In a recent study published in Advanced Theory and Simulations, a team of scientists led by Prof. Maezono and his colleague, Keishu Utimula, Ph.D. in material science from JAIST (In 2020) and first author of the study, proposed an approach based on statistical randomness to identify G for sample sizes much larger (~ trillion) than lmax. The idea, essentially, is to pick a sample of size l that is much smaller than L, identify M(l) using machine-learning "clustering," and repeat the process by varying l. As l increases, the estimated M(l) converges to M(L) or G, provided G is considerably smaller than lmax (which is almost always satisfied). However, this is still a computationally expensive strategy, because it is tricky to know exactly when convergence has been achieved.
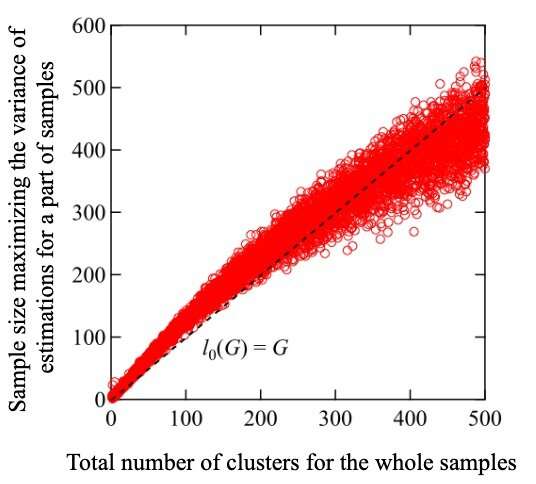
To address this issue, the scientists implemented another ingenious strategy: They made use of the "variance," or the degree of spread, in M(l). From simple mathematical reasoning, they showed that the variance of M(l), or V[M(l)], should have a peak for a sample size ~ G. In other words, the sample size corresponding to a maximum in V[M(l)] is approximately G. Furthermore, numerical simulations revealed that the peak variance itself scaled as 0.1 times G, and was thus a good estimate of G.
While the results are yet to be mathematically verified, the technique shows promise of finding applications in high-performance computing and machine learning. "The method described in our work has much wider applicability than Polya's theorem and can, therefore, handle a broader category of problems. Moreover, it only requires a machine learning clustering tool for sorting the data and does not require a large memory or whole sampling. This can make AI recognition technology feasible for larger data sizes even with small-scale recognition tools, which can improve their convenience and availability in the future," says Prof. Maezono.
More information: Keishu Utimula et al, Stochastic Estimations of the Total Number of Classes for a Clustering having Extremely Large Samples to be Included in the Clustering Engine, Advanced Theory and Simulations (2021). DOI: 10.1002/adts.202000301