Computer scientists develop model that explains how collective scenarios such as diseases may proceed

It is winter, the typical time for colds. What if you could simulate how the disease may spread? At the Cluster of Excellence Collective Behavior at the University of Konstanz, Julia Klein, a doctoral student in computer science, and colleagues investigated how using strict, rule-based methods can help better estimate the parameters for Markov chains. The findings are published in the journal PLOS ONE.

Markov chains are a specific stochastic model with which we analyze populations over discrete time periods. The researchers studied scenarios where only a limited sample of population-level data measurements is available for the analysis. Not having the full range of data is a common situation for experimental research in biology and therefore represents an essential research interest.

The formal verification method by Klein can, for example, be used for predicting disease spread. In this case, the available measurement data at the population level is only a snapshot of the situation at a fixed point in time. When looking at a sample situation of a completed wave of a disease on a specific date, each person could be in one of three stages: healthy, ill, or recovered.

"Once this information is available, we can infer the rates of infection and recovery, and use the resulting model to simulate how the situation will develop over a longer period for different population sizes," says Klein.

Many other collective phenomena can be simulated with this model. The researchers used it, for example, to look at the stinging behavior of honeybees. They found out that the larger the swarm, the less willing the bees are to sting.

Klein and her colleagues have developed the method because stochastic population models are widely used to model phenomena in different areas such as cyber-physical systems, chemical kinetics or collective animal behavior. However, there are limits as Klein says, "Quantitative analysis of stochastic population models easily becomes challenging due to the combinatorial number of possible states of the population.

"Moreover, although it is easy for the person creating the model to propose how different parts of the model are connected, it is hard or sometimes impossible to directly measure the numbers that describe these connections."

A new, more accurate method?

The computer scientists propose and implement four different case studies, including the disease spread model and the model for the social feedback mechanism in honeybee colonies.

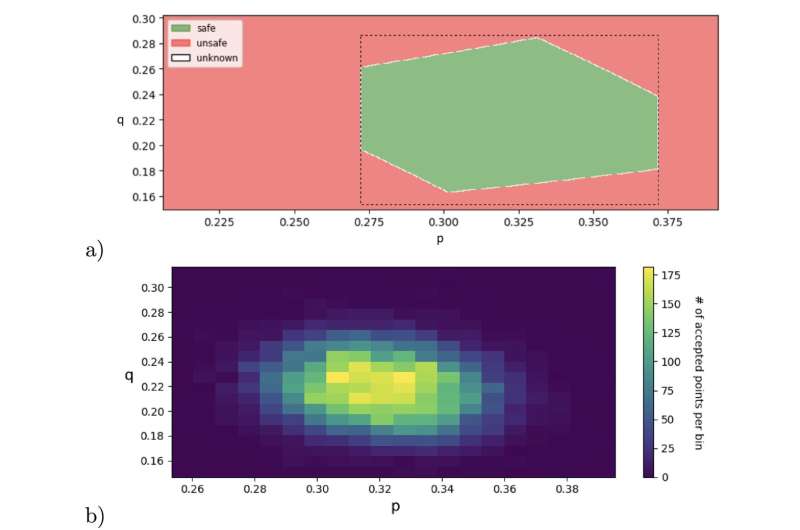
Based on the case studies, Tatjana Petrov, a professor of computer science, says, "We find that the proposed methods incorporating formal parameter synthesis as a pre-computation step allow us to significantly enhance the accuracy, precision and scalability of the inferences. Specifically, in the case of unidentifiable parameters, we accurately capture the subspace of parameters which is data-compliant at a desired level of confidence."