When Waddington meets Helmholtz: EPR-Net for constructing the potential landscapes of complex non-equilibrium systems

The concept of Waddington landscape, originally proposed by British developmental biologist Conrad Hal Waddington in 1957, has been influential in describing the dynamical evolution of cellular development.

Waddington's metaphor of a ball rolling down a hill to represent cell differentiation has been widely adopted in epigenetics and developmental biology. However, quantitative characterization of these landscapes, particularly for high-dimensional systems, remains a challenging problem in computational biology.

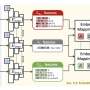
Led by Professor Tiejun Li (from Peking University) and Dr. Wei Zhang (from Freie Universität Berlin and Zuse Institute Berlin), together with Yue Zhao (first author, Ph.D. student from Peking University), a recent study published in the journal National Science Review introduces EPR-Net, a deep learning method that effectively tackles this challenge.

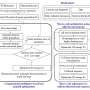
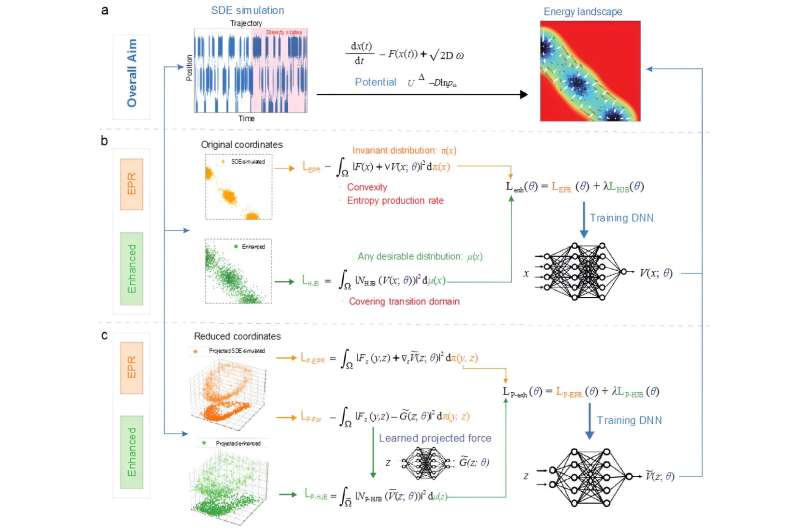
This method leverages the unique mathematical insight that the negative gradient of the Waddington landscape corresponds to an extended Helmholtz decomposition in the context of non-equilibrium systems. This insight, closely related to the entropy production rate (EPR) in statistical physics, is a breakthrough that has not been recognized previously.

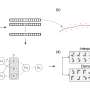
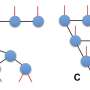
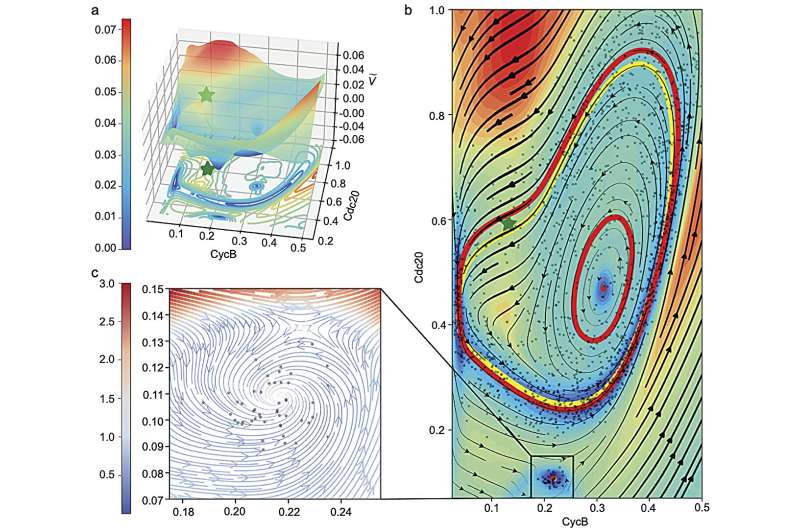
The research team demonstrates the power of EPR-Net through its application to various biological models, including those exhibiting multiple stable points, limit cycles, and strange attractors. Enhanced EPR-Net, an extension of the method, is also introduced.

The study showcases the effectiveness of enhanced EPR on benchmark problems and its superiority over other methods. It also provides a unified framework to address landscape construction, dimensionality reduction, and problems with variable coefficients.

EPR-Net offers computational efficiency, eliminates the need for boundary conditions, and provides a clear physical interpretation that links directly to the entropy production rate in statistical physics.

To address the challenge of visualizing high-dimensional landscapes, the researchers also developed a dimensionality reduction strategy using EPR-Net. This strategy has been applied to study an 8-dimensional limit cycle system, where it gives accurate projections that not only closely match the system's equilibrium distribution but also reveal new delicate structures not observed before.

"EPR-Net, with its elegant mathematical foundation and convex structure, promises to be an effective strategy for constructing energy landscape functions of high-dimensional NESS systems," The researchers conclude. "We are currently exploring further extensions and applications of the method. We feel excited because this powerful method has the potential to improve our understanding of many complex NESS systems by visualizing their potential landscapes."