August 14, 2018 feature
DeepMind researchers develop neural arithmetic logic units (NALU)
The ability to represent and manipulate numerical quantities can be observed in many species, including insects, mammals and humans. This suggests that basic quantitative reasoning is an important component of intelligence, which has several evolutionary advantages.
This capability could be quite valuable in machines, enabling faster and more efficient completion of tasks that involve number manipulation. Yet, so far, neural networks trained to represent and manipulate numerical information have rarely been able to generalize well outside of the range of values encountered during the training process.
A team of researchers at Google DeepMind have recently developed a new architecture that addresses this limitation, achieving better generalization both inside and outside the range of numerical values on which the neural network was trained. Their study, which was pre-published on arXiv, could inform the development of more advanced machine learning tools to complete quantitative reasoning tasks.
"When standard neural architectures are trained to count to a number, they often struggle to count to a higher one," Andrew Trask, lead researcher on the project, told Tech Xplore. "We explored this limitation and found that it extends to other arithmetic functions as well, leading to our hypothesis that neural networks learn numbers similar to how they learn words, as a finite vocabulary. This prevents them from properly extrapolating functions requiring previously unseen (higher) numbers. Our objective was to propose a new architecture which could perform better extrapolation."
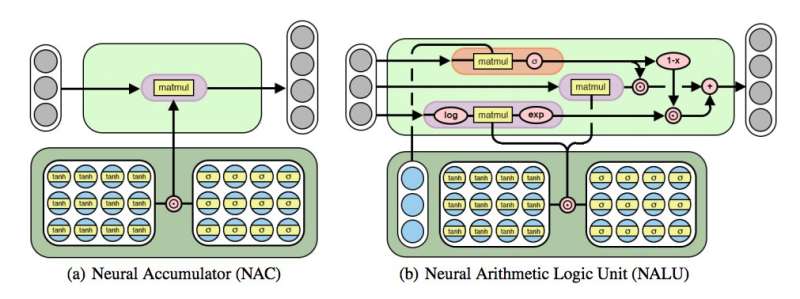
The researchers devised an architecture that encourages a more systematic number extrapolation by representing numerical quantities as linear activations that are manipulated using primitive arithmetic operators, which are controlled by learned gates. They called this new module the neural arithmetic logic unit (NALU), inspired by the arithmetic logic unit in traditional processors.
"Numbers are usually encoded in neural networks using either one-hot or distributed representations, and functions over numbers are learned within a series of layers with non-linear activations," Trask explained. "We propose that numbers should instead be stored as scalars, storing a single number in each neuron. For example, if you wanted to store the number 42, you should just have a neuron containing an activation of exactly '42,' instead of a series of 0-1 neurons encoding it."
The researchers have also changed the way in which the neural network learns functions over these numbers. Rather than using standard architectures, which can learn any function, they devised an architecture that forward propagates a pre-defined set of functions which are seen as potentially useful (e.g. addition, multiplication or division), using neural architectures that learn attention mechanisms over these functions.
"These attention mechanisms then decide when and where each potentially useful function can be applied instead of learning that function itself," Trask said. "This is a general principle for creating deep neural networks with a desirable learning bias over numerical functions."
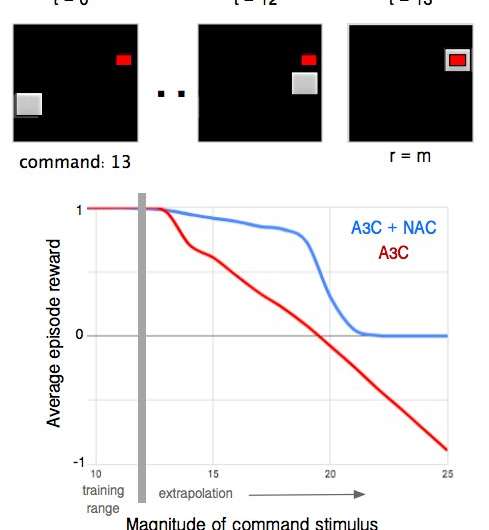
Their test revealed that NALU-enhanced neural networks could learn to perform a variety of tasks, such as time tracking, performing arithmetic functions over images of numbers, translating numerical language into real-valued scalars, executing computer code and counting objects in images.
Compared to conventional architectures, their module attained significantly better generalization both inside and outside the range of numerical values it was presented with during training. While NALU might not be the ideal solution for every task, their study provides a general design strategy for creating models that perform well on a particular class of functions.
"The notion that a deep neural network should select from a predefined set of functions and learn attention mechanisms governing where they are used is a very extensible idea," Trask explained. "In this work, we explored simple arithmetic functions (addition, subtraction, multiplication and division), but we are excited about the potential to learn attention mechanisms over much more powerful functions in the future, perhaps bringing the same extrapolation results we have observed to a wide variety of fields."
More information: Neural Arithmetic Logic Units. arXiv: 1808.00508v1 [cs.NE]. arxiv.org/abs/1807.09882
Abstract
In this paper, we examine the visual variability of objects across different ad categories, i.e. what causes an advertisement to be visually persuasive. We focus on modeling and generating faces which appear to come from different types of ads. For example, if faces in beauty ads tend to be women wearing lipstick, a generative model should portray this distinct visual appearance. Training generative models which capture such category-specific differences is challenging because of the highly diverse appearance of faces in ads and the relatively limited amount of available training data. To address these problems, we propose a conditional variational autoencoder which makes use of predicted semantic attributes and facial expressions as a supervisory signal when training. We show how our model can be used to produce visually distinct faces which appear to be from a fixed ad topic category. Our human studies and quantitative and qualitative experiments confirm that our method greatly outperforms a variety of baselines, including two variations of a state-of-the-art generative adversarial network, for transforming faces to be more ad-category appropriate. Finally, we show preliminary generation results for other types of objects, conditioned on an ad topic.
© 2018 Tech Xplore