Mathematics to keep farmers on track
Scientists at the Tokyo University of Agriculture and Technology (TUAT) used nonlinear mathematical modeling to understand the bouncing and sliding instabilities that can lead to tractor accidents. This research may help protect farmers from injury, as well as better control automated agricultural systems.
The research was published in Biosystems Engineering on Feb 12th, 2020 as "Numerical analysis of steering instability in an agricultural tractor induced by bouncing and sliding."
Accidents in which tractors overturn are a leading cause of death for farmers. This is especially concerning in regions that have uneven terrain. Repeated bumps of a specific frequency can lead to catastrophic bouncing or sliding instabilities. This resonant frequency reflects the natural oscillation period of the tractor, but when applied from an outside source, can cause vibrations with dangerously large amplitudes. Similar to an earthquake that can topple one building while leaving neighboring structures undamaged, one tractor may be safe to ride a certain route while another will be in danger of overturning. Moreover, even a slight increase in speed may start violent vibrations that cause the front wheels to lift off the ground, preventing proper steering.
The TUAT researchers used a mathematical bicycle model that represented the front and back wheels of the tractor as damped oscillators, and calculated the vertical and pitching motion of a trailing implement, such as a rotary tiller. The equations allowed the computer to calculate the motions of each component as part and simulate the overall stability based on the parameters of the system, like the stiffness of the wheel springs. Using frequency response analysis, which involved intensive numerical experiments for various parameter combinations, they showed that the stability of the tractor was strongly dependent on specific conditions, especially the travel speed of the tractor and the friction coefficient of the road. "As in many non-linear systems, the onset of instability is very sensitive to the control parameters," says first author Masahisa Watanabe. This means that small changes in velocity and friction coefficient can lead to a discontinuous increase in bouncing and sliding.
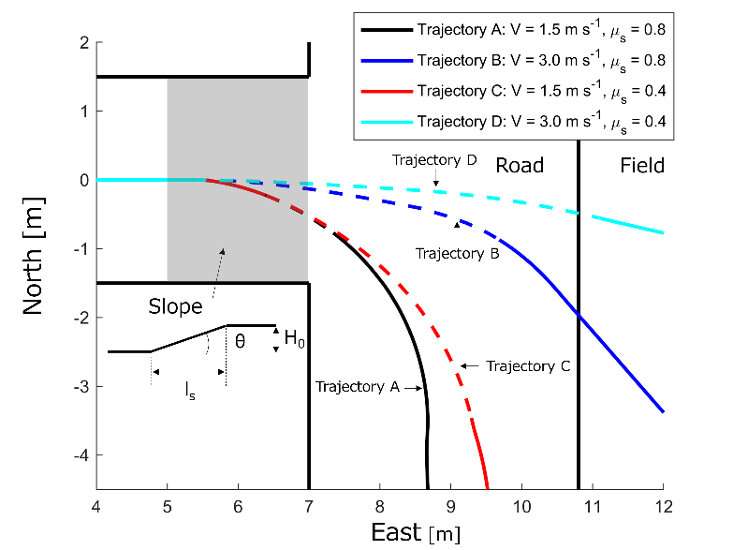
"We included simulations based on actual accident case studies in Japan, and found that a large increase in nonlinear response can happen when the tractor attempts to climb a 19-degree slope," says senior author Kenshi Sakai. The right figure shows the tractor trajectories in the numerical experiments of the tractor operations on the passage slope of 19 degree. In the numerical experiments, the travel velocity V was respectively set at 1.5 and 3.0 m s-1 for the low and high velocity conditions and the static friction coefficient μs was respectively set at 0.8 and 0.4 for the preferable and adverse road conditions. When the travel velocity V was 1.5 m s-1, Trajectories A and C remained on the road throughout the simulation while there was steering instability for Trajectory C. When the travel velocity was V = 3.0 m s-1, the tractor trajectory dramatically deviated outward for Trajectories B and D. In particular, for Trajectory D, the steering instability continued until the tractor reached the edge of the road.
This project aims not only to protect the safety of farmers, but also to advance the understanding of autonomous control theory.
More information: Masahisa Watanabe et al, Numerical analysis of steering instability in an agricultural tractor induced by bouncing and sliding, Biosystems Engineering (2020). DOI: 10.1016/j.biosystemseng.2020.01.014