Julia programming language tackles differential equation challenges
Emerging open-source programming language Julia is designed to be fast and easy to use.
Since it is particularly suited for numerical applications, such as differential equations, scientists in Germany are using it to explore the challenges involved in transitioning to all-renewable power generation.
Decarbonization implies a radical restructuring of power grids, which are huge complex systems with a wide variety of constraints, uncertainties, and heterogeneities. Power grids will become even more complex in the future, so new computational tools are needed.
In Chaos, Potsdam Institute for Climate Impact Research (PIK) scientists describe a software package they built to enable the simulation of general dynamical systems on complex networks.
They wanted to build an open-source tool—so anyone can verify its software structure and algorithms—to make all state-of-the-art algorithms within Julia's ecosystem easily accessible to engineers and physicists. Their package, called NetworkDynamics.jl, started out as the computational backend of another one, PowerDynamics.jl.
"We realized our computational backend would be useful to other researchers within the dynamical systems community as well," said Michael Lindner, a postdoctoral researcher at PIK.
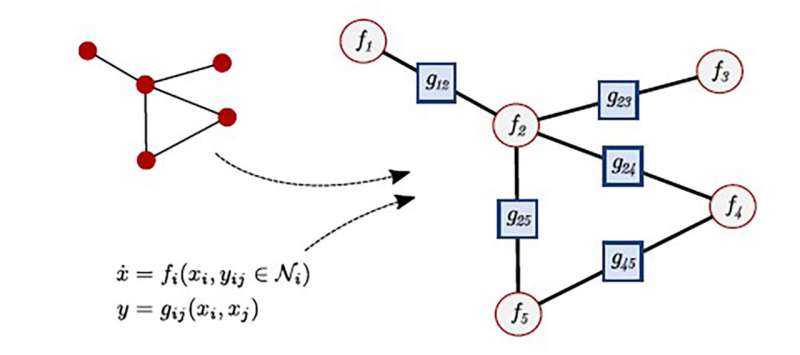
The two theoretical pillars of their work are differential equations and complex networks.
"By casting models of power grids or brains, for example, in terms of differential equations on networks, we give them a clear underlying structure," he said. "The network encodes locality, what interacts with what, and the differential equations encode dynamics, how things change with time."
This enables researchers to obtain state-of-the-art simulation speeds.
"We first compute all the interactions among network components, then the back reactions of individual components to that interaction. This allows us to compute the entire evolution of the system within two easily parallelizable loops," said Lindner.
Since Julia is fast and easy to write and has a library for solving differential equations (DifferentialEquations.jl), researchers can implement and simulate complicated models within one day—rather than the month it used to require with other languages.
"It removes some of the barriers limiting scientific creativity," Lindner said. "I hadn't even thought about certain models and important questions before, just because they seemed completely out of reach with my given time constraints and programming skills."
A good, intuitive interface to high-performance algorithms is "important for science today," he said, "because they enable scientists to focus on their research questions and models instead of code and implementation details."
More information: "NetworkDynamics.jl - Composing and simulating complex networks in Julia," Chaos, aip.scitation.org/doi/10.1063/5.0051387