September 7, 2021 feature
The realization of an Ising Hamiltonian solver based on coupled phase-transition nano-oscillators
Combinatorial optimization problems are a class of hard computational problems that are commonly solved by computers for a variety of applications. Combinatorial optimization algorithms, for instance, allow economists to make predictions about a given market or help streaming platforms to recommend other suitable movies for individual users based on their past activity.
The more complex a combinatorial problem becomes, the greater computational power and resources will be required to solve it. Over the past few years, engineers and computer scientists have thus been trying to develop devices and platforms that could solve this type of computational problems faster and more efficiently, ranging from optical to electronic and quantum techniques.
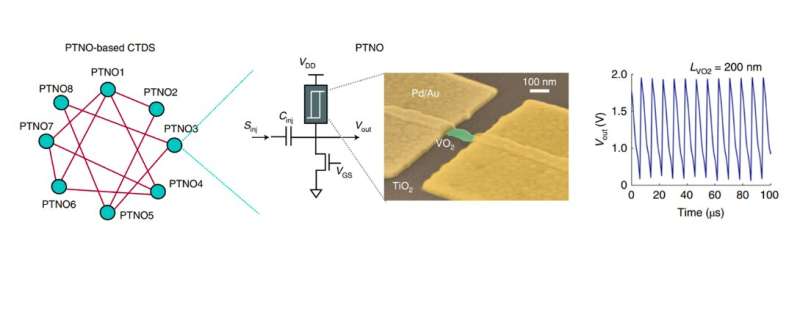
Researchers at University of Notre Dame, Georgia Institute of Technology and Cornell University have recently developed an Ising Hamiltonian solver that may solve combinatorial optimization problems more efficiently that many existing devices. This solver, presented in a paper published in Nature Electronics, is based on coupled stochastic phase-transition nano-oscillators (PTNOs), a class of nanoscalerelaxation oscillators that resemble very much spiking neurons in biology.
"The primary inspiration for our research came from two seminal works by computer scientists John Hopfield, Geoffrey Hinton and David Ackley working with biophysicists David Tank and Terence Sejnowski in 1985," Prof. Suman Datta, principal investigator for the study, told TechXplore. "They put forward the idea of a massively parallel and highly interconnected network of nonlinear elements such as binary neurons, capable of performing extremely powerful and yet energy-efficient computing, also known as collective computing."
In the highly interconnected network of nonlinear elements described by Hopfield, Hinton and their colleagues, the computational power lies within the dense connectivity between the computing elements. The massively parallel network they describe could therefore be well-suited for solving combinatorial optimization problems that belong to the so-called non-deterministic polynomial (NP)-hard or to the NP-complexity classes, as solving these problems entails identifying a single optimal solution among billions of possible candidates.
"Building on this idea, we developed a novel hardware of coupled PTNOs that can perform massively parallel searches through nearly all possible candidates and return the correct solution with an energy dissipation and run-time that is more than 10,000x lower than using our desktop computers," Sourav Dutta, a post-doctoral researcher involved in the study, told TechXplore.
A tool that can efficiently solve highly complex combinatorial optimization numbers with countless possible solutions could be of great value in numerous settings. Its many possible applications range from drug discovery to cryptography, quantitative finance, resource allocation and trajectory planning for autonomous vehicles or robots.
As part of their study, Prof. Datta, Dutta and their colleagues used the classical Ising model, a mathematical model devised by physicists Ernst Ising and Wilhelm Lenz, to find the minimum energy configuration of a large system comprised of many interacting magnetic spins. As the Ising model is a so-called "NP-complete' problem, countless real-world optimization problems can be converted into an Ising problem, including Boolean satisfiability and graph partitioning. This makes the solver developed by the researchers relevant across a broad range of problems.
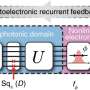
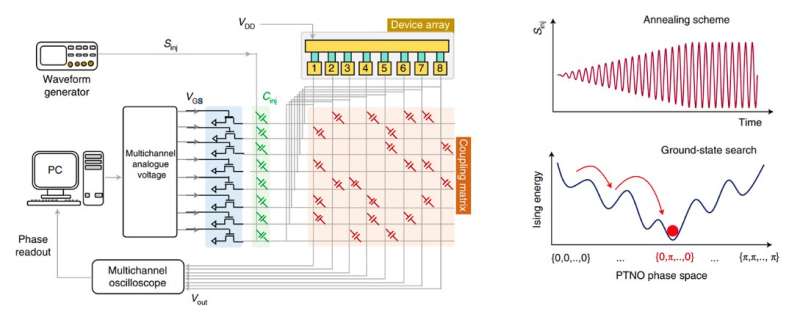
"We developed a fast and energy efficient hardware platform using coupled phase-transition nano-oscillators (PTNOs) that can solve the Ising problem and many other optimization problems," Abhishek Khanna, a Ph.D. student at University of Notre Dame involved in the study, told TechXplore. "The PTNOs are biased by an external modulating signal to produce two phases which behave like up and down magnetic spins, using a phenomenon known as injection locking."
A key aspect of the processes carried out by the researchers' solver is the mapping of the Ising problem onto the device's hardware. Prof. Datta, Dutta and Khanna achieved this by connecting the oscillators using simple electrical elements, such as resistors and capacitators. When the oscillators are connected, the energy cost function of this interacting network is defined by an equation called the "Ising Hamiltonian."
"The phases of each oscillator in the network evolve parallelly over time such that the Ising Hamiltonian of the network reaches a minimum value," Khanna explained. "This value corresponds to the optimum solution of a given opimization problem."
An important characteristic feature of the solver developed by the team is that it possesses an in-built stochasticity or randomness that can be tuned using an external electrical signal. This is a crucial step in ensuring that the trajectory of the dynamics of coupled oscillators evolves towards the global optimum solution and does not get stuck on the other nearby countless possibilities.
"The advantage of our Ising Hamiltonian solver's hardware is the ability to perform massively parallel searches through nearly all possible candidates and return the correct solution with an energy dissipation and run-time that are over 10,000x lower than that achieved using common desktop computers," Dutta said.
The researchers evaluated their solver's performance and efficiency in a series of tests. Their results are highly promising, as they found that a prototype of their solver comprised of eight PTNOs could solve an NP-hard MaxCut problem with a 96% probability of success for 600 annealing cycles.
"Through experimental demonstration and rigorous mathematical treatment, this work lays a foundation for utilizing the continuous-time dynamics of an interacting network of coupled non-linear oscillators to perform parallel computation and solve mathematically challenging combinatorial optimization problems," Dutta said. "From a practical implementation perspective, the key figure-of-merits for an Ising solver include the size of the hardware, operating temperature and the time and energy spent in obtaining the solution of the optimization problem."
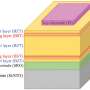
The Ising Hamiltonian solver developed by Prof. Datta, Dutta, Khanna and their colleagues can operate at room temperature and is fast, accurate and energy efficient. In addition, to make it more compact, the researchers exploited the intriguing phenomenon of insulator-to-metal phase transition that occurs in complex correlated oxide materials fabricate highly compact and low-power nanoscale non-linear oscillators that can be coupled to each other using simple electrical elements.
"A major challenge for collective computing is to implement the massive amount of interconnection among the computing elements that can be reconfigured on-the-fly to solve a wide range of problems," Dutta added. "While the number of non-linear oscillators required to solve a problem grows linearly with the problem size, the number of connections grows quadratically O(N2). From an engineering perspective, the challenge lies in realizing such a massive connectivity in a compact foot-print area on-chip without losing signal fidelity or slowing down the entire network."
To realize such large-scale connectivity among different computing elements, the researchers are now working on two different innovations. Firstly, they are working to introduce new non-volatile transistor elements with programmable conductances that could be used as coupling elements.
"In addition, we aim to stack these programmable coupling elements in the vertical direction on top of the nonlinear oscillators in multiple tiers which paves the way for a fully monolithic 3D integration solution," Khanna said. "This will allow us to densely pack large-scale networks on-chip, thereby reducing the silicon real estate while boosting the chip performance."
More information: S. Dutta et al, An Ising Hamiltonian solver based on coupled stochastic phase-transition nano-oscillators, Nature Electronics (2021). DOI: 10.1038/s41928-021-00616-7
© 2021 Science X Network