Neural networks make sense of complex electron interactions
Researchers from the Center for Materials Technologies at Skoltech have delivered a proof-of-concept demonstration of a neural network-driven method for creating a precise exchange-correlation functional interpolation, which is the core component of density functional theory. DFT, in turn, is the main numerical method used in condensed matter physics and quantum chemistry to calculate compound reactivity, the zonal structure of molecules, the durability of materials, and other properties crucial for the search for new materials, drugs, and more. The promising neural network architecture was presented and analyzed in Scientific Reports.
As described by the multielectron Schrödinger equation, the motions of electrons in matter determine the properties of the electronic structure. For example, the chemical bond, a core concept of all chemistry, is a complex correlated motion of electrons governed by the laws of quantum mechanics.
The problem with the multielectron Schrödinger equation is that while it is relatively easy to state, no analytical solution has been found, and the numerical solution is highly complex and challenging. Here, one of the main approaches is the medium field (density) method, which describes the complex interaction of electrons in terms of an effective potential.
"The density functional theory simplifies things by using the notion of an electron cloud characterized by certain local density instead of considering individual electrons," the first author of the study, Skoltech Research Engineer Alexander Ryabov, explained.
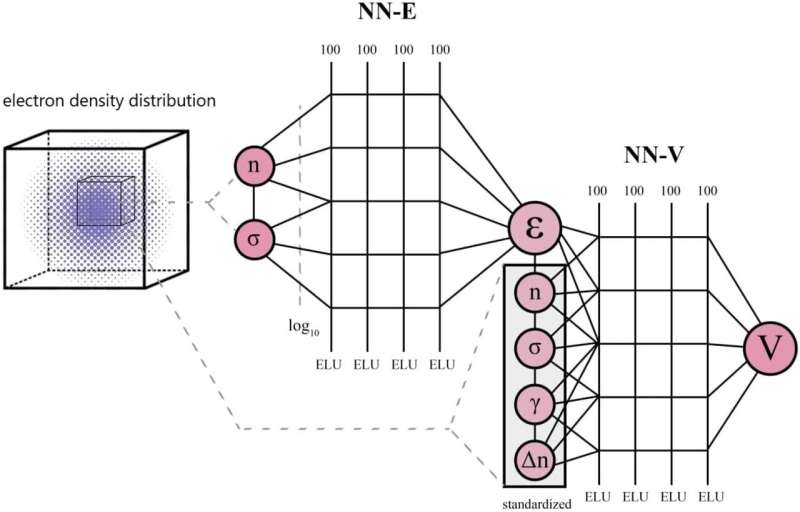
"However, this theory has an important unknown value, called the exchange-correlation functional. Until recently, the tendency was to approximate it analytically. That is, coefficients in the functional form were determined based on several known physical principles without recourse to neural networks. Our method is the first to use a two-component neural network for this. Neural networks have been actively employed in this task, but our team is pioneering them in this area in Russia."
According to the researchers, what sets theirs apart from the competing approaches is that training happens in two stages: First, one network is trained, and its weights are frozen. Then another one is taught.
"Previously, people used a neural network to approximate the exchange-correlation functional, after which computationally intensive derivatives had to be taken to find the corresponding exchange-correlation potential. These are derivatives of a kind that often proves hard to compute with decent accuracy using a neural network," Skoltech Senior Research Scientist Petr Zhilyaev, the study's principal investigator, added. "In our work, a two-component neural network approximates both the potential and the functional, so no complicated derivatives are involved, and the computational load is diminished."
"To run the experiments reported in our paper, we implemented the neural network into the Octopus software suite for quantum chemistry," Ryabov said. "We also investigated how the training process is affected by non-self-consistent densities. After adding such densities into the training dataset, we observed improved performance on molecules for which the neural network previously produced the worst results."
More information: Alexander Ryabov et al, Application of two-component neural network for exchange-correlation functional interpolation, Scientific Reports (2022). DOI: 10.1038/s41598-022-18083-1