An algorithm for optimal decision making under heavy-tailed noisy rewards

In data science, researchers typically deal with data that contain noisy observations. An important problem explored by data scientists in this context is the problem of sequential decision making. This is commonly known as a "stochastic multi-armed bandit" (stochastic MAB).
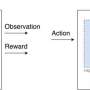
Here, an intelligent agent sequentially explores and selects actions based on noisy rewards under an uncertain environment. Its goal is to minimize the cumulative regret–the difference between the maximum reward and the expected reward of selected actions. A smaller regret implies a more efficient decision making.
Most existing studies on stochastic MABs have performed regret analysis under the assumption that the reward noise follows a light-tailed distribution. However, many real-world datasets, in fact, show a heavy-tailed noise distribution. These include user behavioral pattern data used for developing personalized recommendation systems, stock price data for automatic transaction development, and sensor data for autonomous driving.
In a recent study, Assistant Professor Kyungjae Lee of Chung-Ang University and Assistant Professor Sungbin Lim of the Ulsan Institute of Science and Technology, both in Korea, addressed this issue. In their theoretical analysis, they proved that the existing algorithms for stochastic MABs were sub-optimal for heavy-tailed rewards.
More specifically, the methods employed in these algorithms—robust upper confidence bound (UCB) and adaptively perturbed exploration (APE) with unbounded perturbation—do not guarantee a minimax (minimization of maximum possible loss) optimality.
"Based on this analysis, minimax optimal robust (MR) UCB and APE methods have been proposed. MR-UCB utilizes a tighter confidence bound of robust mean estimators, and MR-APE is its randomized version. It employs bounded perturbation whose scale follows the modified confidence bound in MR-UCB," explains Dr. Lee, speaking of their work, which was published in IEEE Transactions on Neural Networks and Learning Systems.
The researchers next derived gap-dependent and independent upper bounds of the cumulative regret. For both the proposed methods, the latter value matches the lower bound under the heavy-tailed noise assumption, thereby achieving minimax optimality. Further, the new methods require minimal prior information and depend only on the maximum order of the bounded moment of rewards. In contrast, the existing algorithms require the upper bound of this moment a priori–information that may not be accessible in many real-world problems.
Having established their theoretical framework, the researchers tested their methods by performing simulations under Pareto and Fréchet noises. They found that MR-UCB consistently outperformed other exploration methods and was more robust with an increase in the number of actions under heavy-tailed noise.
Further, the duo verified their approach for real-world data using a cryptocurrency dataset, showing that MR-UCB and MR-APE were beneficial–minimax optimal regret bounds and minimal prior knowledge–in tackling heavy-tailed synthetic and real-world stochastic MAB problems.
"Being vulnerable to heavy-tailed noise, the existing MAB algorithms show poor performance in modeling stock data. They fail to predict big hikes or sudden drops in stock prices, causing huge losses. In contrast, MR-APE can be used in autonomous trading systems with stable expected returns through stock investment," says Dr. Lee, discussing the potential applications of the present work.
"Additionally, it can be applied to personalized recommendation systems since behavioral data shows heavy-tailed noise. With better predictions of individual behavior, it is possible to provide better recommendations than conventional methods, which can maximize the advertising revenue," he concludes.
More information: Kyungjae Lee et al, Minimax Optimal Bandits for Heavy Tail Rewards, IEEE Transactions on Neural Networks and Learning Systems (2022). DOI: 10.1109/TNNLS.2022.3203035