This article has been reviewed according to Science X's editorial process and policies. Editors have highlighted the following attributes while ensuring the content's credibility:
fact-checked
peer-reviewed publication
trusted source
proofread
A new twist on a classic math formula speeds work with looping structures

Scientists often turn to origami for tasks like packing expandable structures into spacecraft or creating new medical devices, but the math used to describe the folds between segments can be difficult to work with. Now, Princeton researchers have developed a new mathematical approach that makes dealing with troublesome folds far easier.
Typical methods treat a crease as a break between two distinct sections of a structure. The methods require engineers to model creases as rotational hinges with certain stiffness and impose geometric and mechanical matching conditions for connecting the two distinct sections of the structure. These models can be resource-intensive to use and don't always capture what happens to a material when it is sharply bent.
"When people study creases it is challenging because there is a discontinuity between sections of the structure," said Sigrid Adriaenssens, a professor of civil and environmental engineering who led the research team. "Normally, they cut it up and impose complicated boundary conditions to represent the discontinuity."
In an article in the Proceedings of the National Academy of Sciences, Adriaenssens's team presents a method that describes creases as part of a continuous system rather than a separate section of calculations. The new method not only allows engineers to conduct calculations in one effort, it also accounts for different degrees of folding in a structure, from sharp tent-like creases to more gradual curves.
"We can model the entire range, from very sharp all the way to very smooth," said Tian Yu, the paper's lead author and an associate research scholar in the Department of Civil and Environmental Engineering.
The researchers said they developed the method by applying a classical math approach more typically used in signal processing and the study of shock waves. Yu said that he had been trying other approaches without success when co-researcher Francesco Marmo suggested applying a function that is a regularized version of the Dirac delta function introduced by mathematician Paul Dirac in 1927. Marmo, of the University of Naples Federico II in Italy, was working at Princeton at the time as part of a Global Collaborative Network program administered by the Princeton Institute for International and Regional Studies.
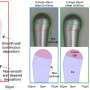
The researchers applied the new system to structures made of looping rings called creased annuli. By varying twists in the rings, the researchers created a wide variety of three-dimensional shapes. Using the new math system, they were able to recreate the structures accurately with a computer.
The article, "Continuous modeling of creased annuli with tunable bistable and looping behaviors" was published Jan. 20 in the Proceedings of the National Academy of Sciences.
More information: Tian Yu et al, Continuous modeling of creased annuli with tunable bistable and looping behaviors, Proceedings of the National Academy of Sciences (2023). DOI: 10.1073/pnas.2209048120