This article has been reviewed according to Science X's editorial process and policies. Editors have highlighted the following attributes while ensuring the content's credibility:
fact-checked
trusted source
proofread
Algorithm is able to learn and preserve the conservation laws of dynamical systems

Many real-world systems, from climate systems to the physical mechanisms of robots, are governed by the invariant quantities that arise from their underlying geometric structures. Modeling these systems using computer simulations is a key tool for understanding them (for weather forecasting, for instance, or developing robot locomotion). It's often possible to collect data for these systems, but making sense of that data to build a model is a more challenging task.
Artificial intelligence has long been used to analyze the data of systems with known conservation laws. However, in the real world, these laws are often unknown. To address this problem, researchers from Osaka University developed an algorithm named FINDE, which not only finds the quantities of known laws, but also those of unknown ones, which could lead to scientific discoveries. The article, "FINDE: Neural Differential Equations for Finding and Preserving Invariant Quantities," will be presented at the 2023 International Conference on Learning Representations.
FINDE assumes invariant quantities and projects the dynamics into the tangent space of a manifold defined by the quantities. This allows FINDE to learn these dynamics and invariant quantities jointly, preserving the conservation laws. Real-world systems are continuous systems, but numerical computer algorithms can only model discrete systems, which can lead to errors and ultimately reduce the accuracy of simulations. Hence, FINDE also uses discrete gradients, which are defined in discrete time, to define the discrete counterpart of the tangent space, and then it can be used without accumulating errors.
"Because FINDE learns and preserves the conservation laws of a system," says Prof. Takashi Matsubara, first author of the study, "our computer simulations will be more accurate over the long term."
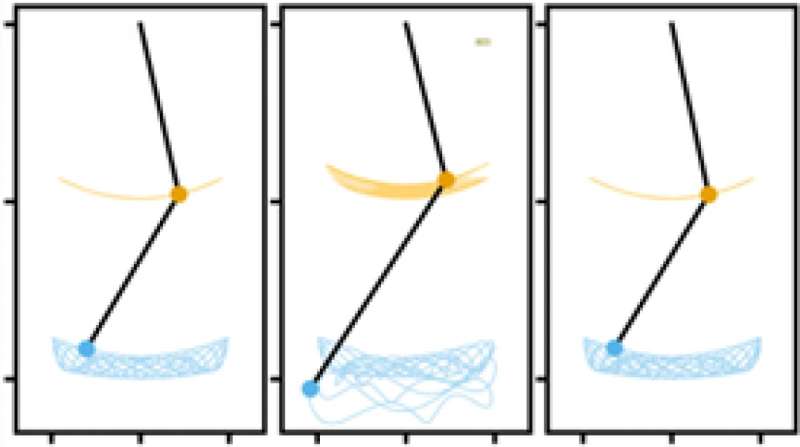
However, FINDE is about more than just reducing modeling errors. If the laws governing a system are unknown, the number of laws might also be unknown. FINDE can be used to determine this number by testing the accuracy of models with different numbers of laws. "This reveals additional information about the underlying structure of a system," says Prof. Matsubara, and that could lead to scientific discoveries about the systems under study.
The researchers tested the ability of FINDE to discover and model systems on a variety of datasets. A two-body gravitational system, shallow water waves, a double pendulum, and the electrical circuit model of a biological neuron were all considered. FINDE was able to find and preserve the first integrals that arise from the conservation laws governing these systems in all cases. As a result, FINDE is expected to contribute to the acceleration and sophistication of future computer-aided engineering and physics simulations.