Solving computationally complex problems with probabilistic computing

According to computational complexity theory, mathematical problems have different levels of difficulty in the context of their solvability. While a classical computer can solve some problems (P) in polynomial time—i.e., the time required for solving P is a polynomial function of the input size—it often fails to solve NP problems that scale exponentially with the problem size and thus cannot be solved in polynomial time. Classical computers based on semiconductor devices are, therefore, inadequate for solving sufficiently large NP problems.

In this regard, quantum computers are considered promising as they can perform a large number of operations in parallel. This, in turn, speeds up the NP problem-solving process. However, many physical implementations are highly sensitive to thermal fluctuations. As a result, quantum computers often demand stringent experimental conditions such extremely low temperatures for their implementation, making their fabrication complicated and expensive.

Fortunately, there is a lesser-known and as-yet underexplored alternative to quantum computing, known as probabilistic computing. Probabilistic computing utilizes what are called "stochastic nanodevices," whose operations rely on thermal fluctuations, to solve NP problems efficiently. Unlike in the case of quantum computers, thermal fluctuations facilitate problem solving in probabilistic computing. As a result, probabilistic computing is, in fact, easier to implement in real life.

Shedding much-needed light on this potential alternative, a group of researchers have now demonstrated the capabilities of probabilistic computing by simulating stochastic nanodevice networks to solve specific NP problems. The study, led by Professor Peter Bermel from Purdue University, is published in the Journal of Photonics for Energy (JPE).

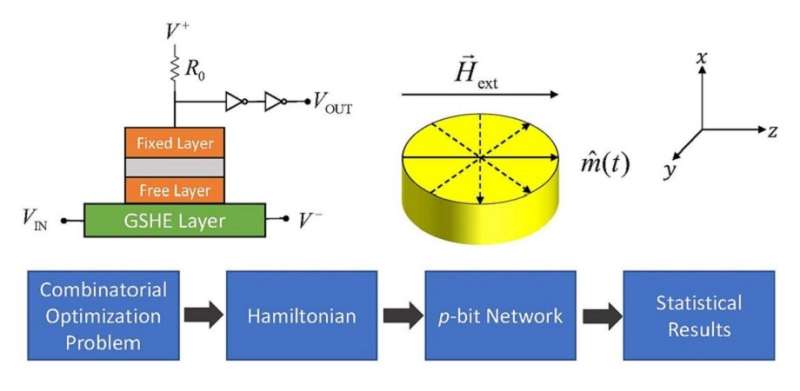
The researchers used the "Ising model," a canonical model for simulating a wide variety of physical as well as mathematical problems. Originally devised to model the interactions of magnetic dipole moments of atomic spins, its energy operator, namely the "Hamiltonian," can also represent NP problems. Essentially, solving an NP problem amounts to solving the corresponding Ising Hamiltonian. Probabilistic computing devices made of networks of optical parametric oscillators (OPOs) and stochastic circular nanomagnets with low thermal barriers have been used to solve such problems.

The researchers implemented one such nanomagnet network using existing fabrication methods. They then used it to solve the Ising Hamiltonians of four NP-complete problems (problems with no efficient solution algorithm) from number theory associated with combinatorial optimization. These included number partitioning, exact cover, binary integer linear programming, and integer linear programming.

The simulation results of the first three problems with 3, 3, and 6 probabilistic bits (p-bits) strongly agreed with the theoretical solution (Boltzmann law) of the Ising model. The researchers observed a similar agreement between modeling and theory in the simulations of five different exact cover problems with 3, 6, 9, 12, and 15 p-bits. This indicated the potential for scaling up probabilistic computing frameworks.

According to Bermel, "in probabilistic computing, efficient scaling with problem size is the key to make it a robust, relevant alternative to classical computing techniques. Both modeling and experiments will be needed to confirm which approaches are most promising."

While the simulation results reported show robust results for all p-bits (from 3 to 15), the researchers suggest that parallel algorithms could help further scale up the simulation capability. In cases where parallelism is not feasible, transitioning from nanomagnet to OPO networks could facilitate efficient problem solving. The system can be mapped on an OPO network and easily implemented with current fabrication techniques, such as the CMOS technology. This, in turn, can lead to the development of stochastic nanomagnets with low energy barriers for probabilistic computing.

JPE Editor-in-Chief Sean Shaheen of University Colorado Boulder remarks, "Developing unconventional forms of computing hardware is becoming increasingly important as AI and scientific/enterprise computing accelerate in scale, at a pace that brings significant—if not urgent—concerns about their energy consumption and carbon footprint."

"This work by Zhu, Xi, and Bermel provides a practical pathway to a hardware platform that solves an important class of NP-complete problems. By creatively harnessing networks of nonlinear optical devices to carry out Ising computing, the work demonstrates a scalable, energy-efficient approach that has the potential to vastly outperform conventional hardware in solving computationally complex problems."