March 28, 2022 feature
A new approach to tackle optimization problems using Boltzmann machines
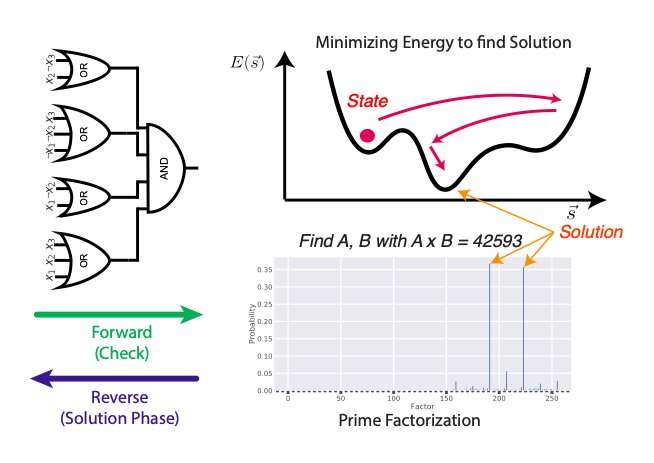
Ising machines are unconventional computer architectures based on physics principles, named after the German physicist Ernst Ising. In recent years, they have been found to be particularly promising tools for solving combinatorial optimization (CO) problems and create artificial models of the brain.
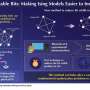
A team of researchers in the group of Sayeef Salahuddin, a TSMC distinguished Professor of EECS at the University of California, Berkeley, has recently been exploring the potential of Ising machines for finding solutions to complex optimization problems in great depth. Their most recent paper, published in Nature Electronics, introduced a new Ising machine comprised of many restricted Boltzmann machines (RBMs), which was found to achieve remarkable results on complex combinatorial optimization tasks.
"In the recent years, a lot of work has gone into Ising machines to accelerate optimization problems, which our work builds on," Saavan Patel, the lead author who carried out the study, told TechXplore. "The primary objectives of our study were to show how machine learning and hardware acceleration can fit into the framework of Ising machines and accelerate optimization problems in a way that is inspired by digital logic."
Restricted Boltzmann machines (RBMs) are generative, stochastic models based on artificial neural networks. These models can be very good at capturing complex correlations and distribution patterns in large amounts of input data.
RBMs rely on binary activations, circumventing the direct matrix-vector multiplications that are typically the most computationally demanding for deep learning networks. In their study, Patel and his colleagues exploited this unique characteristic of the models to increase the speed at which their machine could solve optimization problems.
"Our algorithm functions by using the basic principles of digital logic in a new way," Patel explained. "Usually, digital gates only function in the forward direction, but by using probabilistic graphical models and machine learning, we have shown ways of operating them in reverse. Using this principle, we design our probabilistic digital circuits in a way that can solve the forward problem ("Is this set of inputs a valid solution?" or "What is 191 x 223?"), but because the system is reversible, it can also answer the much harder reverse problem ("What are all the sets of inputs that produce a valid solution?" and "What are A and B such that A x B = 42593?" )."
The machine they developed allowed Patel and his colleagues to solve a variety of different optimization problems. Essentially, their circuit works by initially evaluating different existing solutions and then trying to identify new solutions itself. In contrast with other previously proposed solutions, the researchers' platform combines problem mapping approaches, machine learning, and hardware solutions together.
"Using our digital logic approach, we were able to show that we could solve two types of 'hard' problems," Patel said. "The first is the boolean satisfiability, which forms the backbone of combinatorial optimization problems, and the second is the integer factorization problem which is the basis for the RSA cryptography algorithm that modern computers use. The goal was to show that this tool works, and we showed that we could solve larger factorization problems than previously proposed methods."
In initial evaluations, the machine created by this team of researchers achieved highly promising results, solving complex combinatorial optimization and integer factorization problems. In addition, the supporting hardware introduced in the paper could find solutions to problems 10000 times faster than a conventional CPU.
In the future, Ising machines like the one introduced by Patel and his colleagues could be used to solve a wide range of complex real-world problems more rapidly and efficiently, including issues associated with logistics or manufacturing, routing problems, and cryptography breaking. In their next studies, the researchers will try to upscale their machine so that it can complete increasingly larger and more complex optimization tasks. In addition, they would like to assess its potential for solving other types of problems.
"We are designing larger and more efficient FPGA systems to solve bigger problems, as well as ASICs," Patel added. "In terms of new problem domains, we have been investigating mappings for routing problems (like the traveling salesman problem), communications problems (like LDPC coding), quantum problems (like finding the ground state of molecular systems), and other optimization problems (e.g., solutions for MAX-CUT problems). There are a lot of new frontiers for these systems and we are excited to explore new spaces! Our goal is to always solve harder problems, faster and more power efficiently."
More information: Saavan Patel et al, Logically synthesized and hardware-accelerated restricted Boltzmann machines for combinatorial optimization and integer factorization, Nature Electronics (2022). DOI: 10.1038/s41928-022-00714-0
© 2022 Science X Network