The solution space of the spherical negative perceptron model is star-shaped, researchers find

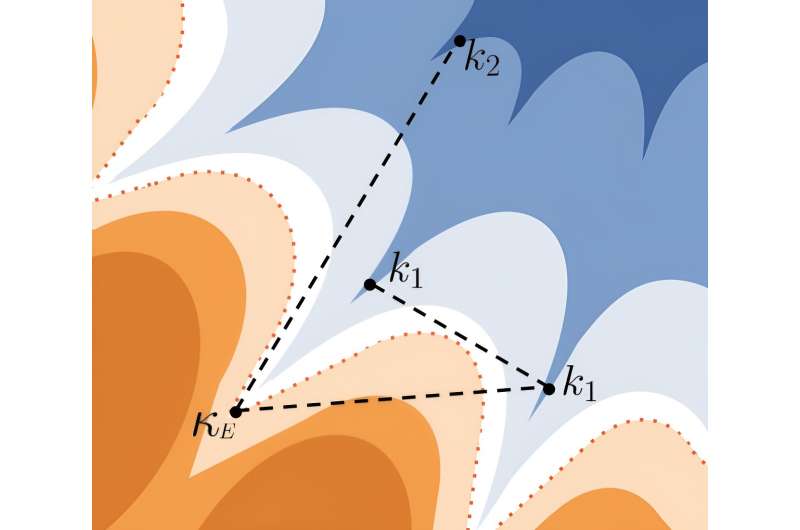
Recent numerical studies investigating neural networks have found that solutions typically found by modern machine learning algorithms lie in complex extended regions of the loss landscape. In these regions, zero-energy paths between pairs of distant solutions can be established.

Researchers at Bocconi University, Politecnico di Torino and Bocconi Institute for Data Science and Analytics recently carried out a study aimed at exploring these regions using one of the simplest non-convex neural network models, known as the negative spherical perceptron. Their paper, published in Physical Review Letters, found that solutions of this neural network model are arranged in a star-shaped geometry.

"Recent research on the landscape of neural networks has shown that independent stochastic gradient descent (SGD) trajectories often land in the same low-loss basin, and often no barrier is found along the linear interpolation between them," Luca Saglietti, co-author of the paper, told Tech Xplore. "We started to think if we could reproduce analytically this phenomenology in a simple model of neural network."

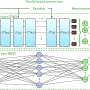
In their paper, Saglietti and his colleagues introduced an analytical method that can be used to compute energy barriers on the linear interpolation between pairs of solutions. As part of their recent study, they applied this method to the so-called spherical negative perceptron , which is essentially a paradigmatic toy model of a neural network.

"This model is particularly interesting because it is both continuous and non-convex," Clarissa Lauditi, co-author of the paper said. "It involves a set of parameters (called weights) that need to be tuned in such a way to satisfy a training set of input-output associations. In the negative perceptron the constraints can be relaxed, and in this overparameterized regime the geometry of the solution space becomes surprisingly rich."

The researchers probed this model and the rich solution landscape associated with it by characterizing the energy barriers on the linear interpolation between pairs of solutions using the so-called replica method. This is a well-known and established technique that is commonly applied in statistical physics studies.

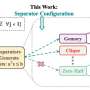
"Unexpectedly, we unveiled that the solutions are arranged in a star-shaped geometry," Enrico Malatesta, co-author of the paper said.

"Most of them are located on the tips of the star, but there exists a subset of solutions (located in the core of the star) that are connected through a straight line to almost all the other solutions. We have found that this shape actually impacts the behavior of the training algorithms: common algorithms used in deep learning have a bias towards the solutions located in the core of the star. Those solutions have desirable properties, e.g. better robustness and generalization capabilities."

The recent work by this research team offers interesting new insight about the geometrical shape of solutions associated with the spherical negative perceptron. The team found that the way the solutions are arranged affects the performance of algorithms, with the algorithms often preferentially selecting solutions located at the center of the star-like geometry, which often exhibit advantageous characteristics.

"Our future research aims to understand to what extent the star-shaped geometry may be a universal property of overparameterized neural networks and weakly constrained optimization problems," Gabriele Perugini, co-author of the paper added. "The possibility that also completely different non-convex optimization problems can develop simple connectivity properties when overparameterized is certainly intriguing."

© 2024 Science X Network