PIANO: A new operator learning framework that deciphers and incorporates invariants from the PDE series

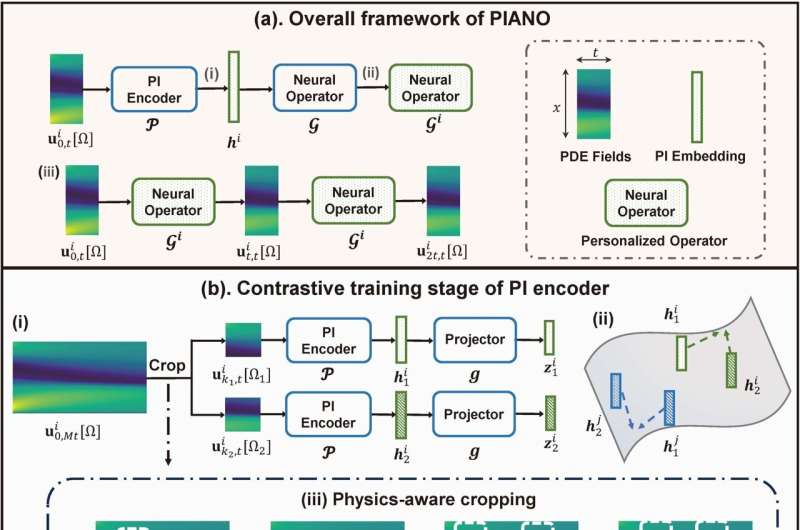
In a recent article published in the National Science Review, researchers have proposed a new operator learning framework called PIANO. PIANO uses self-supervised learning to extract representations containing physical invariants from partial differential equations (PDEs) systems with different physical mechanisms, thereby extending the generalization ability of neural operators to various physics scenarios.

This study was led by Prof. Zhi-Ming Ma (Academy of Mathematics and Systems Science (AMSS), the Chinese Academy of Sciences) and Dr. Qi Meng (Microsoft Research AI4Science). Ph.D. student Rui Zhang from AMSS is the first author.

Neural operators regard training PDE solvers as learning a mapping from function to function, thereby significantly accelerating the simulation process. Compared with traditional methods, neural operators break through the limitations of space-time discretization, increase the inference speed by thousands of times, and show great potential in fields such as inverse design and physical simulation.

However, most current methods mainly consider data from systems driven by a single equation, which limits the application of neural operators in multi-physics scenarios.

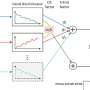
To solve this problem, researchers have proposed a new operator learning framework called Physical Invariant Attention Neural Operator (PIANO). PIANO can decipher and integrate physical knowledge from PDE series data driven by various physical invariants, such as parameters and boundary conditions of equations.

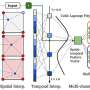
PIANO adopts two key designs: One is to use self-supervised learning methods to learn representations containing physical invariants, and the other is to embed the learned representations into neural operators through dynamic convolution layers. In addition, researchers have proposed three types of physics-aware cropping methods based on prior knowledge to align with the attributes of different PDE systems.

Researchers have demonstrated the effectiveness and physical significance of PIANO on several benchmark problems, including Burgers' equation, convection-diffusion equation, and Navier-Stokes equation. The experimental results show that when PIANO learns neural operators from PDE datasets with various physical mechanisms, its accuracy and generalization are better than existing methods.

According to the results of six experiments, PIANO can reduce the relative error rate by 15.1%–82.2% by deciphering and integrating the physical information of the PDE system. Furthermore, the results of a series of downstream tasks verify the physical significance of the extracted PI representation by PIANO.