Porous-DeepONet: A deep learning framework for efficiently solving reaction-transport equations in porous media

Porous media play a critical role in various industrial fields due to their complex pore networks and considerable specific surface areas. The transport and reaction phenomena within porous media are key factors influencing fundamental parameters such as energy storage efficiency, catalytic performance, and adsorption rates.

To accurately describe these complex transport and reaction processes, solving parameterized partial differential equations (PDEs) is necessary. However, due to the complex structure of porous media, traditional methods, such as the finite element method (FEM), require substantial computational resources.

There is an urgent need for innovative methods to accelerate the solution of parameterized PDEs in porous media.

Researchers have developed a novel deep operator network, Porous-DeepONet, which can efficiently capture the complex features of porous media and thereby more precisely and effectively learn the solution operators, providing a robust alternative for solving parameterized reaction-transport equations in porous media and paving the way for exploring complex phenomena within them.

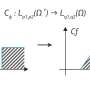
Deep operator networks (DeepONet) are a popular deep learning framework often used to solve parameterized PDEs. However, applying DeepONet to porous media presents significant challenges due to its limited ability to extract representative features from complex structures.

To address this issue, researchers proposed Porous-DeepONet, a simple yet efficient extension of the DeepONet framework that utilizes convolutional neural networks (CNNs) to learn the solution operators of parameterized reaction-transport equations in porous media. The work is published in the journal Engineering.

By incorporating CNNs, Porous-DeepONet can effectively capture the complex features of porous media, achieving accurate and efficient learning of the solution operators. Additionally, researchers have coupled Porous-DeepONet with other DeepONet frameworks to extend its applicability to solving multiphysics coupled equations in porous media, resulting in Porous-DeepM&Mnet and Porous-PI-DeepONet, which are based on physical information.

To validate the effectiveness of Porous-DeepONet in accurately and rapidly learning the solution operators of parameterized reaction-transport equations under various boundary conditions, multiphase, and multiphysics fields, researchers conducted a series of comprehensive numerical simulations.

The results demonstrate that Porous-DeepONet has the capability to accurately capture system behavior under various challenging conditions, showcasing its practical application potential for simulating complex porous media with different reaction parameters and boundary conditions.

Compared to traditional FEM methods, Porous-DeepONet is three orders of magnitude faster at solving the same problems. Furthermore, when Porous-DeepM&Mnet is used to solve the Poisson–Nernst–Planck (PNP) equations, the solution speed is improved by approximately 50 times.

Porous-DeepONet has thus become a powerful tool for addressing the solution of parameterized PDEs in porous media, especially excelling in handling complex domain geometries and multiphysics coupled equations. This research provides strong support for further exploration and application in related fields.

In summary, this work introduces Porous-DeepONet, a deep learning framework designed to learn solution operators for parameterized PDEs in porous media, with a focus on reaction-transport equations.

Compared to traditional FEM, this extension can significantly improve solving efficiency. To assess the accuracy and applicability of Porous-DeepONet, researchers solved various reaction-transport equations, including the Fick diffusion equation, Fick diffusion and surface reaction equations, advection equations, and heat conduction equations.

The results indicate that Porous-DeepONet efficiently solves single-phase and multiphase parameterized PDEs with complex boundary conditions, with computation times three orders of magnitude faster than traditional FEMs.

Additionally, by combining Porous-DeepONet with DeepM&Mnet to address the challenge of solving multiphysics coupled PNP equations, computation times were dramatically reduced by a factor of 50.

With improvements and optimizations, Porous-DeepONet has become a powerful tool for solving parameterized PDEs in porous media, particularly excelling in handling complex domain geometries and multiphysics coupled equations. This research provides strong support for further exploration and application in related fields.