June 20, 2019 feature
Using game theory to model poisoning attack scenarios
Poisoning attacks are among the greatest security threats for machine learning (ML) models. In this type of attack, an adversary tries to control a fraction of the data used to train neural networks and injects malicious data points to hinder a model's performance.
Although researchers have been trying to develop techniques that could detect or counteract these attacks, the effectiveness of these techniques often depends on when and how they are applied. In addition, sometimes applying filtering techniques to screen ML models against poisoning attacks can reduce their accuracy, preventing them from analyzing both genuine and corrupt data.
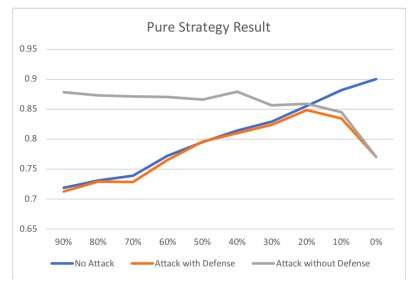
In a recent study, researchers at McMaster University in Canada have successfully used game theory to model poisoning attack scenarios. Their findings, outlined in a paper pre-published on arXiv, proves the nonexistence of a pure strategy Nash equilibrium, which entails each player repeatedly choosing the same strategy in the attacker and defender "game."
Studying the behaviors of both attackers and defenders when poisoning attacks take place could help to develop ML algorithms that are more protected against them and yet retain their accuracy. In their study, the researchers tried to model poisoning attacks within the context of game theory, a branch of mathematics concerned with better understanding strategies used in competitive situations (e.g. games), where an outcome greatly depends on the choices of those involved (i.e. participants).
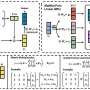
"The objective of this paper is to find the Nash equilibrium (NE) of the game model of poisoning attack and defense," Yifan Ou and Reza Samavi, the two researchers who carried out the study, explain in their paper. "Identifying the NE strategy will allow us to find the optimal filter strength of the defending algorithm, as well as the resulting impact to the ML model when both the attacker and the defender are using optimal strategies."
In game theory, NE is a stable state of a system that involves competitive interactions between different participants (e.g. a game). When NE occurs, no participant can gain anything by a unilateral change of strategy if the strategy of the other player/players remain unchanged.
In their study, Ou and Samavi tried to find the NE in the context of poisoning attacks and defense strategies. First, they used game theory to model poisoning attacks dynamics and proved that a pure NE is nonexistent in such a model. Subsequently, they proposed a mixed NE strategy for this particular game model and showed its effectiveness in an experimental setting.
"We used game theory to model the attacker and defender strategies in poisoning attack scenarios," the researchers wrote in their paper. "We proved the nonexistence of the pure strategy NE, proposed a mixed extension of our game model and an algorithm to approximate the NE strategy for the defender, then demonstrated the effectiveness of the mixed defense strategy generated by the algorithm."
In the future, the researchers would like to investigate a more general approach to address poisoning attacks, which entails detecting and rejecting samples using auditing algorithms. This alternative approach might be particularly effective to update and improve a trained model in situations where the users' feedback is sought online.
More information: Mixed strategy game model against data poisoning attacks. arXiv:1906.02872 [cs.LG]. arxiv.org/abs/1906.02872
© 2019 Science X Network