A novel solution to a combinatorial optimization problem in bicycle sharing systems
Bicycle sharing systems have become an attractive option to alleviate traffic in congested cities. However, rebalancing the number of bikes at each port as time passes is essential, and finding the optimal routing paths for the vehicles in charge of rebalancing constitutes a combinatorial optimization problem. Now, scientists propose an innovative algorithm that can find near-optimal solutions more quickly even for a large number of ports, paving the way for more efficient bicycle sharing systems.
Traffic congestion has been worsening since the 1950s in large cities thanks to the exorbitant number of cars sold each year. Unfortunately, the figurative price tag attached to excessive traffic includes higher carbon dioxide emissions, more collectively wasted time, and exacerbated health problems. Many municipalities have tackled the problem of traffic by implementing bicycle sharing systems, in which people can borrow bikes from strategically placed ports and ride wherever they want, as long as they eventually return the bikes to a port, although not necessarily the one from where the bike was originally obtained.
As one may or may not immediately notice, this last permission creates a new problem by itself. Whenever someone borrows a bike and does not make a round trip with it, an additional bike crops up at the destination port just as there's a loss of one bike at the origin port. As time passes, the distribution of bikes across ports becomes unbalanced, causing both an excessive accumulation of bikes at certain ports and a dearth of bikes in others. This issue is generally addressed by periodically sending out a fleet of vehicles capable of transporting multiple bikes in order to restore ports to their 'ideal' number of bikes.
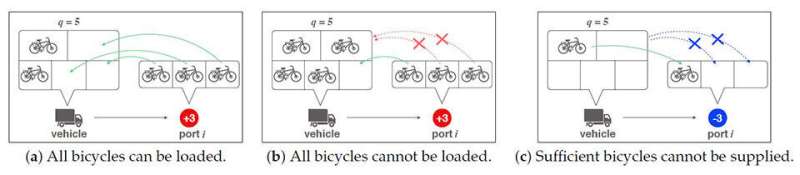
Much research has been dedicated to the bicycle rebalancing problem using a fleet of vehicles. Finding the optimal routing paths for the vehicles is in and of itself a highly complex mathematical problem in the field of combinatorial optimization. One must make sure that the optimization algorithms used can reach a good-enough solution in a reasonable time for a realistically large number of ports and vehicles. Many methods, however, fail to find feasible solutions when multiple constrains are considered simultaneously, such as time, capacity, and loading/unloading constraints for the vehicles (Figure 1).
But what if we allowed the optimization strategy to change the strategies a little bit to make the best out of difficult situations? In a recent study published in MDPI's Applied Sciences, a team of scientists suggested an innovative twist to the routing problem of bicycle sharing systems using this concept. Led by Professor Tohru Ikeguchi of Tokyo University of Science, the team comprising Ph.D. student Honami Tsushima from Tokyo University of Science and Associate Professor Takafumi Matsuura from Nippon Institute of Technology, Japan, proposed a new formulation of the routing problem in which the constraints imposed on the routings can be violated. This enabled using the optimization algorithm for exploring what is known as the space of "infeasible solutions." Prof. Ikeguchi explains their reasoning, "In real life, if a work can be completed through overtime within a few minutes, we would work beyond the time limit. Similarly, if we are only carrying four bikes and need to supply five, we would still supply the four we have."
Following this line of thought, the researchers formulated the "soft constraints" variant of the routing problem in bicycle rebalancing. Using this approach, instead of outright excluding solutions that violate constraints, these can be considered valid paths that incur dynamically adjusted penalties and taken into consideration when assessing possible routings. This approach enabled the team to devise an algorithm that can make use of the space of infeasible solutions to speed up the search for optimal or near-optimal solutions.
The researchers evaluated the performance of their method through numerical experiments with benchmark problems including up to 50 ports and three vehicles. The results show that their strategy could find optimal or near-optimal solutions in all cases, and that the algorithm could search both the feasible and infeasible solution spaces efficiently. This paints a brighter future for people in cities with congested traffic in which bicycle sharing systems could become an attractive solution. As Prof. Ikeguchi remarks, "It is likely that bike sharing systems will spread worldwide in the future, and we believe that the routing problem in bicycle rebalancing is an important issue to be solved in modern societies."
More information: Honami Tsushima et al, Strategy for Exploring Feasible and Infeasible Solution Spaces to Solve a Multiple-Vehicle Bike Sharing System Routing Problem, Applied Sciences (2021). DOI: 10.3390/app11167749