DeepMind's AI system AlphaGeometry able to solve complex geometry problems at a high level

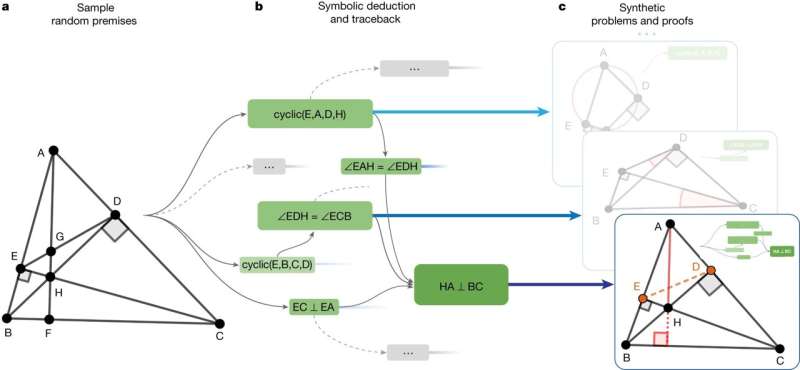
A team of AI researchers at Google's DeepMind, working with a colleague from New York University, has developed an AI system called AlphaGeometry that has demonstrated an ability to solve complex geometry problems at a high level.

In their paper published in the journal Nature, the group describes their new AI system and the ideas they used in its development. The team at Nature has also published a podcast giving an overview of the new AI system.

Proving mathematical theorems can be a challenging endeavor, and people who can do it well are considered to be valuable assets to institutes of higher learning, and in some cases, companies, such as Google. So a means of identifying such individuals has been established—the International Mathematical Olympiad. It is described as the World Championships of Mathematics competitions for high school students.

Because of many of the difficulties inherent in using math for many modern applications, such as the design of computer systems, computer scientists have been hoping for AI systems that can solve complex math problems and/or prove theorems. Unfortunately, up until now, AI systems have not performed nearly as well as hoped. In this new study, however, the team at DeepMind has now created an AI system called AlphaGeometry that competes at the level of gold-medal-winning students in the International Mathematical Olympiad.

To create AlphaGeometry, the research team used a new approach. Rather than attempting to teach the system how to prove theorems using multiple examples, they used a neural language model that allowed the system to train itself. This was done by synthesizing millions of known theorems and proofs with various levels of complexity. They also added a symbolic deduction engine to help the system learn and solve increasingly complex problems without assistance by humans.

The researchers then tested their new system by giving it 30 problems faced by students in the International Mathematical Olympiad over the years 2002 to 2020 and found that it was able to solve 25 of them considerably better than prior AI systems. They noted that its performance was on par with the average gold medalists at the competition.

The research team notes that the system is currently programmed to work with specific forms of geometry but suggests it may be able to expand its repertoire to other domains.

© 2024 Science X Network