January 11, 2023 report
This article has been reviewed according to Science X's editorial process and policies. Editors have highlighted the following attributes while ensuring the content's credibility:
fact-checked
preprint
trusted source
proofread
Modification to Shor's algorithm may mean less powerful quantum computers could crack cryptosystems
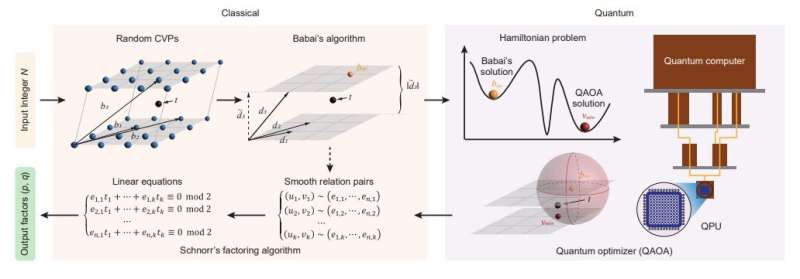
A team of researchers affiliated with a host of institutions across China has modified Shor's algorithm in a way that could allow less powerful quantum computers to crack current cryptosystems. The team describes their modifications and outlines the results of testing it using real-world quantum computers in a paper published on the arXiv preprint server.
In the early 1990s, researchers developed encryption keys for protecting computer systems and data that involved multiplying two prime numbers together. Figuring out which two numbers were used to create a given large number proved to be more than conventional systems could handle as the numbers grew larger.
But then in the mid-'90s, mathematician Peter Shor came up with an algorithm that could be used to crack such cryptosystems using a quantum computer. But since quantum computers of the time, or even those that exist today, have not progressed to the point that they can run the algorithm, cryptography remains secure—but perhaps not for very long.
In this new effort, the researchers have modified Shor's algorithm (they call theirs Schnorr's algorithm) for use on much less powerful quantum computers. Their work involved an optimization algorithm to speed up the processing of the steps that take the most work in the original algorithm, and thus the most time. And they proved it works by factoring a 48-bit number on a quantum computer with just 10 qubits.
They suggest that soon, they will be able to factor much longer numbers, putting conventional cryptosystems at risk. They estimate that a quantum computer using 372 qubits running their algorithm could crack any of the cryptosystems in use today. Not mentioned in their work is one caveat that remains—today's quantum computers have error rates so high that it would be impossible to use them to crack cryptosystems.
If systems with much lower error rates do arise in the near future, cryptosystem makers could increase the size of the prime numbers used to generate their keys—but only for so long. A more likely prospect for securing computer systems in the future will use quantum-secure communications, specifically quantum key distribution.
More information: Bao Yan et al, Factoring integers with sublinear resources on a superconducting quantum processor, arXiv (2022). DOI: 10.48550/arxiv.2212.12372
© 2023 Science X Network