Trajectoids: Creating a shape that rolls along a desired path

Normally, when we think of a rolling object, we tend to imagine a torus (like a bicycle wheel) or a sphere (like a tennis ball) that will always follow a straight path when rolling. However, the world of mathematics and science is always open to exploring new ideas and concepts. This is why researchers have been studying shapes, like oloids, sphericons and more, which do not roll in straight lines.

All these funky shapes are really interesting to researchers as they can show us new ways to move objects around smoothly and efficiently. For example, imagine reducing the energy required to make a toy robot move, or mixing ingredients more thoroughly with a unique-looking spoon. While these peculiar shapes have been studied before, scientists have now taken it a step further.

Consider a game where you draw a path on a tilted table—similar to tilting a pinball table to make the ball go in a particular direction. Now, try to come up with a 3D object that, when placed at the top of the table, will roll down and exactly follow that path, instead of just going straight down. There are a few other rules of this game: the table needs to be inclined slightly (and not too much), there should be no slipping during rolling, and the initial orientation of the object can be chosen at launch. Plus, the path you draw must never go uphill and must be periodic. It must also consist of identical repeating segments—somewhat like in music rhythm patterns.

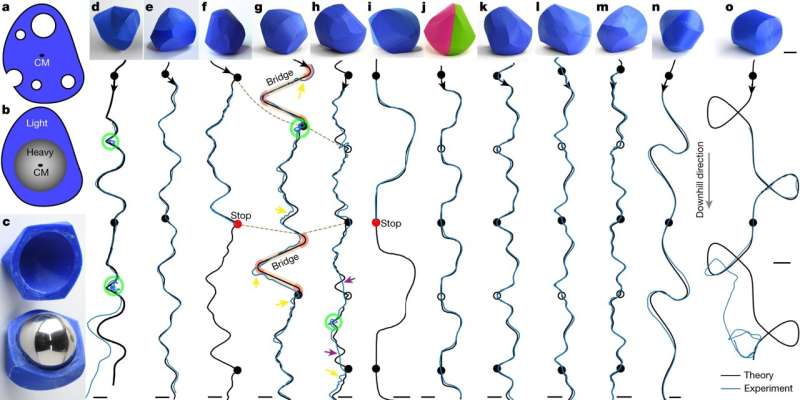
An international team of researchers affiliated with UNIST has pondered whether it's possible to find a winning strategy for this game. They wanted to know if, for any given repetitive path, it would be possible to design a shape that can be rolled to follow this path on its own. The goal was to develop a general recipe that would work not just for simple curves, but also for complicated and intertwined paths. The strangely shaped objects created for this purpose were named "trajectoids."

At first glance, it appears impossible for a 3D object to automatically follow a predetermined rolling path while navigating all the angles and curves. However, the scientists started by simplifying the problem. They envisioned starting with a perfectly smooth basketball covered in flexible, trimmable material, akin to clay. By strategically removing portions of the basketball's cover material that made contact with the table while ensuring the basketball itself always touched the path, it is possible to gradually sculpt the object into a custom shape. This resulting shape would then magically follow the same path when rolling independently. Applying this concept, the scientists successfully devised a new method for creating trajectoids.

These trajectoids aren't just theoretical; the researchers 3D printed them and conducted successful experiments. They even ventured into making trajectoids that occasionally move uphill or follow self-intersecting paths. You can even try the new algorithm yourself for any path you desire, as the researchers have released an online tool for generating 3D-printing-ready files for trajectoids.

For a trajectoid to be successful, it must follow the periodic path indefinitely, maintaining the same orientation each time it completes a certain number of periods. The crucial aspect is how many path periods the trajectoid completes with one "full revolution," thereby restoring its orientation. It's appear highly unlikely to create a trajectoid that completes one revolution for every path period. But on the other hand, the researchers have shown that designing a trajectoid that completes two path periods for each revolution is almost always possible.

This two-periods-per-revolution property is a manifestation of an astonishing general property of rotations in 3D space and can be used in many fields of science where phenomena can be mathematically described as 3D rotations—for example, in quantum computing, quantum optics, and classical optics.

In quantum physics, there's a concept called the "Bloch sphere," which is used to describe quantum states. These states encompass all the possible situations that a quantum system, such as a quantum bit or qubit, can be in. Just as a sphere rolling along a path provides information about its movement at specific points and orientations, the Bloch sphere represents unique qubit states, with changes in these states mirroring the motion of a rolling sphere.

Given this mathematical similarity, scientists can use the same algorithm for designing a trajectoid to help verify the accuracy of quantum computers. Scientists often assess this accuracy by examining how closely a point on the Bloch sphere returns to its original position after specific actions, much like when a trajectoid completes one full revolution and restores its orientation after passing two path periods.

The science of crafting customizable trajectoids is also related to another seemingly unrelated field—disease diagnosis via MRI. "Spin" is a fundamental property of particles like protons, which make up hydrogen atoms in our bodies. Protons behave as tiny magnets, with their "spin" dictating the orientation of their magnetic "north." This property is crucial for Magnetic Resonance Imaging (MRI) machines used in hospitals for patient scans.

To connect this with the Bloch sphere, consider that each point and orientation on the Bloch sphere represents a unique proton spin state, much like our trajectoid's orientation. MRI machines use powerful magnetic fields to align these proton magnets within the body in one direction. Subsequently, they employ radio waves to disrupt this alignment. As the protons naturally realign themselves, they emit signals that can be measured and used to create detailed internal images.

Understanding how each proton returns to its original point on the Bloch sphere helps scientists differentiate human tissues and identify abnormalities. Mathematically, the proton spin state is analogous to the trajectoid's orientation, the radio waves represent the path, and the changes in proton spin caused by the radio waves are equivalent to the rolling motion of the trajectoid along the path.

The mathematics behind the trajectoid algorithm reveal how any given MRI radio wave pulse can be finely tuned, such that repeating the pulse twice in succession restores all proton spins to their original state. This insight could potentially enhance MRI machines and improve disease diagnoses with greater accuracy.