Researchers unveil time series deep learning technique for optimal performance in AI models

A team of researchers has unveiled a time series machine learning technique designed to address data drift challenges. This innovative approach, led by Professor Sungil Kim and Professor Dongyoung Lim from the Department of Industrial Engineering and the Artificial Intelligence Graduate School at UNIST, effectively handles irregular sampling intervals and missing values in real-world time series data, offering a robust solution for ensuring optimal performance in artificial intelligence (AI) models.

The paper is published on the arXiv preprint server.

Time series data, characterized by continuous chronological data collection, is prevalent across various industries, such as finance, transportation, and health care. However, the presence of data drifts—changes in external factors influencing data generation—presents a significant hurdle to leveraging time series data effectively in AI models.

Professor Kim emphasized the critical necessity of combating the detrimental effects of data drift on time series learning models, stressing the urgency of addressing this persistent issue that impedes the optimal utilization of time series data in AI models.

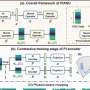
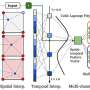
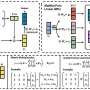
In response to this challenge, the research team has introduced a novel methodology leveraging Neural Stochastic Differential Equations (Neural SDEs) to construct resilient neural network structures, capable of mitigating the impacts of data drifts.

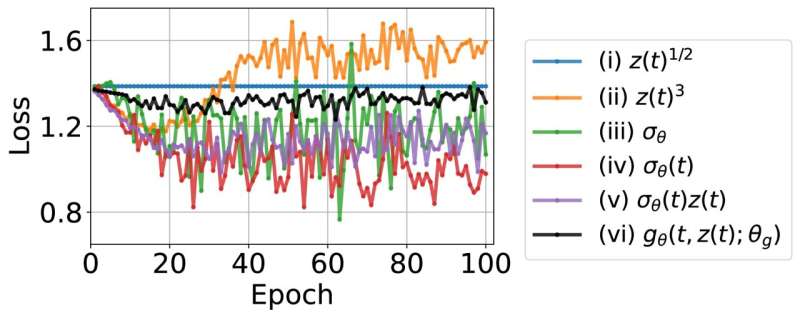
Neural SDEs, an extension of neural Ordinary Differential Equations (ODEs), represent continuous versions of residual neural network models and form the cornerstone of the team's innovative approach. Through the implementation of three distinct neural SDEs models—Langevin-type SDE, Linear Noise SDE, and Geometric SDE—the researchers demonstrated stable and exceptional performance across interpolation, prediction, and classification tasks, even in the presence of data drift.

Traditionally, addressing data drift necessitated labor-intensive and costly engineering adjustments to adapt to evolving data landscapes. However, the team's methodology offers a proactive solution by ensuring AI models remain resilient to data drift from the outset, obviating the need for extensive relearning processes.

Professor Lim underscored the study's significance in fortifying the resilience of time series AI models against dynamic data environments, thereby enabling practical applications across diverse industries. Lead author YongKyung Oh highlighted the team's dedication to advancing technologies for monitoring time series data drift and reconstructing data, paving the way for widespread adoption by Korean enterprises.

This research has been recognized as a top 5% spotlight paper at the International Conference on Learning Representations (ICLR), and it represents a potentially significant advancement in the field of AI and data science.