A novel Kalman filter for target tracking in space

The space station is a bridgehead for human space exploration missions. During its construction, operation, and maintenance, there are a variety of tasks that need to be performed. However, the space environment has harsh conditions such as microgravity, high vacuum, strong radiation, and large temperature differences, which seriously threaten the health and life safety of astronauts.
Since space robots are not limited by human physiological conditions, they can perform space exploration missions for a long time with high quality, which has become an important trend in space exploration. During space station missions, robots need to perform precise operations on tools or task objects, which relies on accurate tracking of the target. However, the special space environment may cause complex non-Gaussian noise in target tracking data. And the performance of a traditional Kalman filter will deteriorate seriously when the error signals are non-Gaussian, which may lead to mission failure.
Therefore, it is necessary to carry out research on filtering algorithms for complex non-Gaussian noises. In a research paper recently published in Space: Science & Technology, a research team combining scholars and scientists from School of Mechatronical Engineering, Beijing Institute of Technology and Hunan University proposed a novel Kalman filter named Generalized Maximum Correntropy Kalman filter (GMCKF) to realize better performance under the non-Gaussian noise with various forms that may encounter in the process of target tracking and to improve the tracking accuracy.
The author first introduced the Generalized Correntropy and analyzed the difference between Gaussian kernel and Generalized Gaussian Density. Existing research focused on improving the Kalman filter's performance under non-Gaussian noise. The Maximum Correntropy Criterion (MCC) has shown good results in evaluating non-Gaussian noise.
There are many filters based on MCC, which can obtain the error's higher-order moments and filter the outliers effectively. However, the default kernel of MCC is a Gaussian kernel. Due to the limit of the Gaussian function, it cannot change the shape of correntropy freely. Therefore, filters like the Maximum Correntropy Kalman filter (MCKF) could not achieve good performance under some complex non-Gaussian noise.
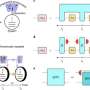
Holding that the Generalized Maximum Correntropy Criterion (GMCC) utilizing the Generalized Gaussian Density (GGD) function has a more flexible form, the author developed a GMCKF algorithm by replacing the Gaussian kernel with a GGD function which adds a new shape parameter α to get better performance under various non-Gaussian noises. Moreover, the author chose the moment-matching estimators (MMEs) to estimate the parameter α because it is simple and accurate enough for parameters estimation.
Afterwards, the influence of the additional shape parameter α and the validity of the parameter automatic selection algorithm for GMCKF were studied in the simulations. It was found through the simulations that with the additional shape parameter α and the automatic selection algorithm, GMCKF can achieve good performance under various non-Gaussian noises. Furthermore, ground experiments have also been done to validate the effect of GMCKF algorithm for target tracking.
The target may be floating in space due to the microgravity environment. In this situation, the vision sensors like cameras in space are exposed to high-energy particles for a long time; there may be complex non-Gaussian noise in the process of image acquisition and transmission. Uncontrolled lighting, coverage by other floating objects, and complex backgrounds can also bring complex non-Gaussian noise to target tracking. To simulate the target tracking in the space environment, the experimental system was built on the base of the Singer model, including a 6-DOF industrial robot (RS10N of Kawasaki), a pair of binocular cameras (MER-125-30UM of Imavision), a spherical target, and a laser tracker.
Because there was not enough complex noise in the laboratory environment, some non-Gaussian noise was deliberately added to the measure data from the binocular camera to simulate the non-Gaussian observation noise generated by various factors in the space station. The experiment results confirmed again that the proposed GMCKF can outperform other filters significantly when the system is disturbed by various non-Gaussian noises. In other words, to get a more accurate target position, the GMCKF algorithm can be used to filter the non-Gaussian noise contained in the target tracking.
Finally, to confirm the algorithm effect in the real environment, the GMCKF algorithm was used to deal with the experimental data from the on-orbit robot maintenance experiments of the Chinese TianGong-2 space laboratory. The purpose of the experiment was to verify that filtering out complex non-Gaussian noise effectively caused by special space environment would help the robot improve its ability to carry out maintenance operations autonomously in the harsh space conditions and complete the task successfully.
The experimental data were transmitted back to the ground from the space laboratory and could be regarded as the real-time measurement data in the true space environment, which verified the algorithm using the practical application data. The experimental results showed that the GMCKF algorithm could help the robot to better locate the target and complete tasks.
More information: Yang Mo et al, Generalized Maximum Correntropy Kalman Filter for Target Tracking in TianGong-2 Space Laboratory, Space: Science & Technology (2022). DOI: 10.34133/2022/9796015