A primal-dual approximation algorithm for the k-prize-collecting minimum vertex cover problem with submodular penalties

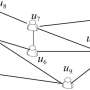
The k-prize-collecting minimum vertex cover problem with submodular penalties (k-PCVCS) is a generalization of the minimum vertex cover problem, which is one of the most important and fundamental problems in graph theory and combinatorial optimization.

This problem is to select a vertex set that covers at least k edges, and the objective is to minimize the total cost of the vertices in the selected set plus the penalty of the uncovered edge set, where the penalty is determined by a submodular function.

To solve the k-PCVCS, Xiaofei Liu et al. published their new research in Frontiers of Computer Science.

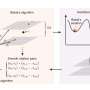
In the research, they first proved that Algorithm 1 can be implemented in O（n¹⁶r+n¹⁷）, where r is the time for one function evaluation. Then, they proved that Algorithm 2 is a 3-approximation algorithm for the k-PCVCS. Specifically, if the penalty function is linear, Algorithm 2 is a 2-approximation algorithm.

Future work may focus on studying the version with general penalties, such as, subadditive or supermodular penalties. Meanwhile, the k-PCVCS with hard capacities deserves to be explored, in which each vertex v is covered at most C_v edges.